giải phương trình: \(4^x-5.2^x+4=0\)
Bài 3: Lôgarit
Đặt \(2^x=t>0\) ta được:
\(t^2-5t+4=0\Rightarrow\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2^x=1\\2^x=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Ac giúp em với, cảm ơn trước ạ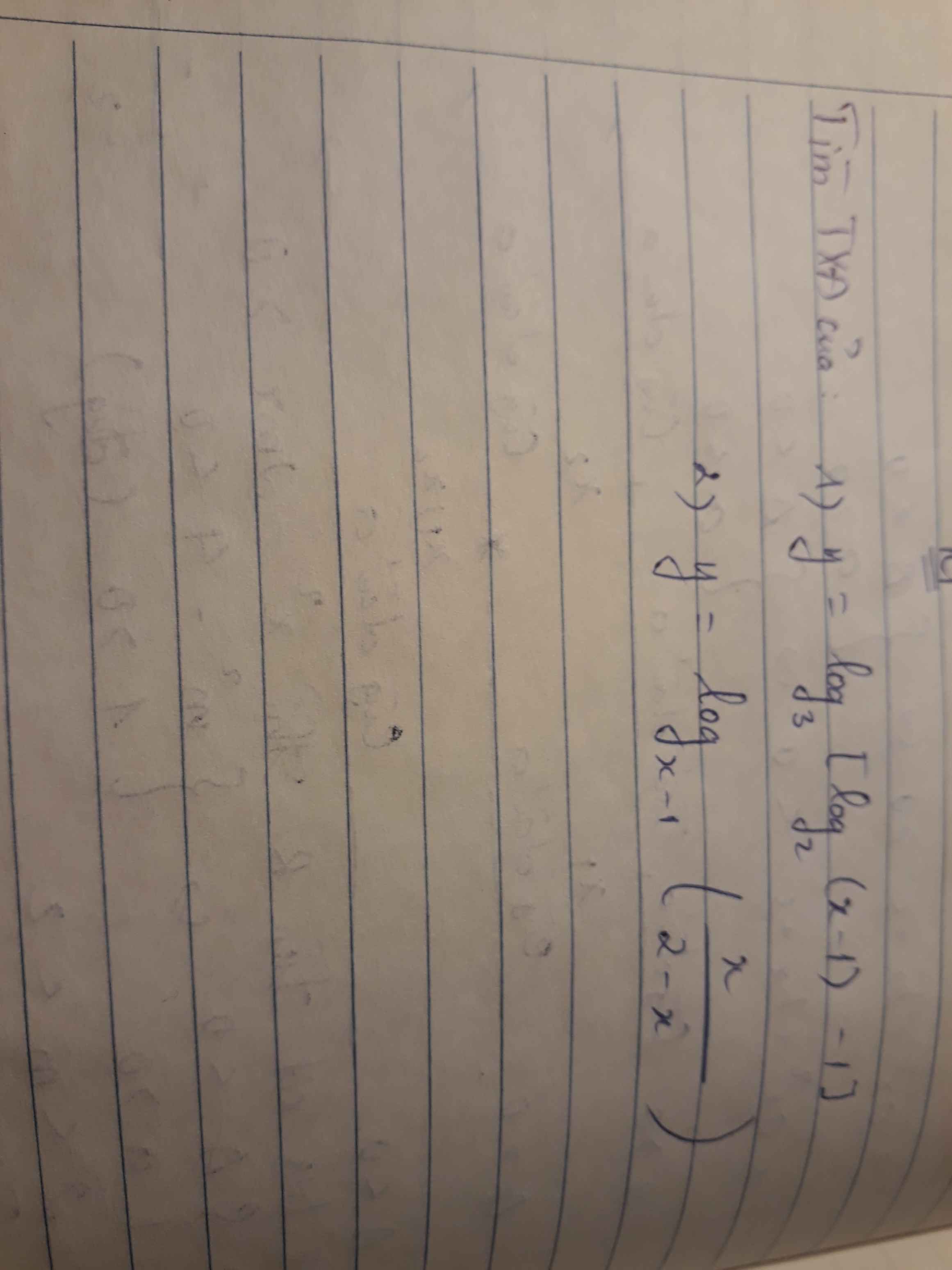
ĐKXĐ:
1.
\(\left\{{}\begin{matrix}x-1>0\\log_2\left(x-1\right)-1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>1\\x-1>2\end{matrix}\right.\) \(\Leftrightarrow x>3\)
2.
\(\left\{{}\begin{matrix}x-1>0\\x-1\ne1\\\dfrac{x}{2-x^2}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>1\\x\ne2\\\left[{}\begin{matrix}x< -\sqrt{2}\\0< x< \sqrt{2}\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow1< x< \sqrt{2}\)
Đúng 1
Bình luận (0)
log5 = a. Tính log\(\dfrac{1}{64}\) theo a
Cho \(a>0\) , \(b>0\) thỏa mãn: \(\log_{3a+2b+1}\left(9a^2+b^2+1\right)+\log_{6ab+1}\left(3a+2b+1\right)=2\) .
Tính giá trị của biểu thức: \(P=a+2b\)
\(a;b>0\Rightarrow3a+2b+1>1\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\) đồng biến
Mà \(9a^2+b^2\ge2\sqrt{9a^2b^2}=6ab\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge2\)
Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}log_{6ab+1}\left(3a+2b+1\right)=1\\3a=b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6ab+1=3a+2b+1\\b=3a\end{matrix}\right.\)
\(\Rightarrow18a^2+1=3a+6a+1\)
\(\Leftrightarrow18a^2-9a=0\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{3}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
y(4x3−2x2+1)2014y(4x3−2x2+1)2014. Đạo hàm y′y′ là:
Đọc tiếp
y=(4x3−2x2+1)2014. Đạo hàm y′ là:
\(16a^2+b^2+1\ge8ab+1\)
\(\Rightarrow log_{4a+5b+1}\left(16a^2+b^2+1\right)+log_{8ab+1}\left(4a+5b+1\right)\ge2\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}b=4a\\4a+5b+1=8ab+1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{4}\\b=3\end{matrix}\right.\)
Đáp án D
Đúng 0
Bình luận (0)
Bài tập 3: Giải phương trình.
a, \(\log_52x-\log_5-x-2=0\)
b, \(9^x-3.3^x+2=0\)
Bạn coi lại đề câu a, chỗ \(\log_5-x\) đó
b.
\(\Leftrightarrow9^x-3^x-2.3^x-2=0\)
\(\Leftrightarrow3^x\left(3^x-1\right)-2\left(3^x-1\right)=0\)
\(\Leftrightarrow\left(3^x-2\right)\left(3^x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3^x=2\\3^x=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\log_32\\x=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Thời gian có hạn copy cái này hộ mình vào google xem nha :
https://lazi.vn/quiz/d/16491/nhac-edm-la-loai-nhac-the-loai-gi
Vào xem xong các bạn nhận được 1 thẻ cào mệnh giá 100k nhận thưởng bằng cách nhắn tin vs mình và 1 phần thưởng bí mật là chiếc áo đá bóng,....
Có 500 giải nhanh nha đã có 200 người nhận rồi. Mình là người phụ trách
OK
Thời gian có hạn copy cái này hộ mình vào google xem nha :
https://lazi.vn/quiz/d/16491/nhac-edm-la-loai-nhac-the-loai-gi
Vào xem xong các bạn nhận được 1 thẻ cào mệnh giá 100k nhận thưởng bằng cách nhắn tin vs mình và 1 phần thưởng bí mật là chiếc áo đá bóng,....
Có 500 giải nhanh nha đã có 200 người nhận rồi. Mình là người phụ trách
OK
log2(4.3x-6)-\(\dfrac{3}{2}\).log2√2(9x-6)=1
Điều kiện xác định : 3\(^x\)>2
Ta có: \(\log_2\left(4.3^x-6\right)=\log_2\left(2\sqrt{2}\right).\log_{2\sqrt{2}}\left(4.3^x-6\right)\)
\(\log_2\left(4.3^x-6\right)-\dfrac{3}{2}\log_{2\sqrt{2}}\left(9^x-6\right)=1\left(1\right)\)\(\Leftrightarrow\log_2\left(2\sqrt{2}\right)\log_{2\sqrt{2}}\left(4.3^x-6\right)-\dfrac{3}{2}\log_{2\sqrt{2}}\left(9^x-6\right)=1\)
\(\Rightarrow\dfrac{3}{2}\log_{2\sqrt{2}}\left(4.3^x-6\right)-\dfrac{3}{2}\log_{2\sqrt{2}}\left(9^x-6\right)=1\)\(\Leftrightarrow\dfrac{3}{2}[\log_{2\sqrt{2}}\left(4.3^x-6\right)-\log_{2\sqrt{2}}\left(9^X-6\right)]=1\)
\(\Leftrightarrow\log_{2\sqrt{2}}\left(\dfrac{4.3^X-6}{9^X-6}\right)=\dfrac{2}{3}\)\(\Leftrightarrow\log_{2\sqrt{2}}\left(\dfrac{4.3^X-6}{9^X-6}\right)=\log_{2\sqrt{2}}\left(2\right)\)
\(\Leftrightarrow\dfrac{4.3^X-6}{9^X-6}=2\Leftrightarrow4.3^X-6=2.9^X-12\)\(\Leftrightarrow2.(3^X)^2-4.3^X-6=0\Rightarrow\left[{}\begin{matrix}3^X=3\left(TM\right)\\3^X=-1\left(loai\right)\end{matrix}\right.\)
\(\Rightarrow x=1.\)Vậy x=1 là nghiệm của phương trình (1)
Đúng 0
Bình luận (0)


