Không sử dụng máy tính, hãy tính :
a) \(\log_2\dfrac{1}{8}\)
b) \(\log_{\dfrac{1}{4}}2\)
c) \(\log_3\sqrt[4]{2}\)
d) \(\log_{0,5}0,125\)
Tính :
a) \(4^{\log_23}\)
b) \(27^{\log_92}\)
c) \(9^{\log_{\sqrt{3}}2}\)
d) \(4^{\log_827}\)
a) \(4^{log^3_2}=\left(2^2\right)^{log^3_2}=\left(2^{log^3_2}\right)^2=3^2=9\).
b) \(27^{log^2_9}=\left(3^3\right)^{log^2_{3^2}}=3^{3.\dfrac{1}{2}.log^2_3}=\left(3^{log^2_3}\right)^{\dfrac{3}{2}}=2^{\dfrac{3}{2}}=\sqrt{8}\).
c) \(9^{log^2_{\sqrt{3}}}=9^{log^2_{9^{\dfrac{1}{4}}}}=9^{4.log^2_9}=\left(9^{log^2_9}\right)^4=2^4=16\).
d) \(4^{log^{27}_8}=2^{2.log^{27}_{2^3}}=2^{\dfrac{2}{3}.log^{27}_2}=\left(2^{log^{3^3}_2}\right)^{\dfrac{2}{3}}=\left(3^3\right)^{\dfrac{2}{3}}=3^2=9\).
Rút gọn biểu thức :
a) \(\log_36.\log_89.\log_62\)
b) \(\log_ab^2+\log_{a^2}b^4\)
a) Từ công thức đổi cơ số suy ra ∀a,b,c > 0 (a,b ≠ 1), logab. logbc = logac.
Do đó log36. log89. log62 = ( log36. Log62). = log32.
log23 =
.
b) logab2+ = logab2 + logab2 =2logab2 = 4 loga|b|.
So sánh các cặp số sau :
a) \(\log_35\) và \(\log_74\)
b) \(\log_{0,3}2\) và \(\log_53\)
c) \(\log_210\) và \(\log_530\)
a) Bằng máy tính cầm tay ta tính được
log35 ≈ 1,464973521; log74 ≈ 0,7124143742,
điều này gợi ý ta tìm cách chứng minh log35 > 1 > log74.
Thật vậy, sử dụng tính chất của lôgarit và tính chất so sánh hai lũy thừa cùng cơ số ta có = 5 > 3 = 31
log35 > 1.
Tương tự 71= 7> 4 =
1> log74. Từ đó log35 > log74.
b) Ta có = 2 >1 =(o,3)0
log0,32 < 0
và = 3 > 1 =50
log53 > 0.
Từ đó log0,32 < log53.
c) = 10 > 23
log210 > 3 và
= 30 < 53
log530 < 3, do đó log210 > log530.
a) Cho \(a=\log_{30}3;b=\log_{30}5\). Hãy tính \(\log_{30}1350\) theo a, b
b) Cho \(c=\log_{15}3\). Hãy tính \(\log_{25}15\) theo c
a) Ta có 1350 = 30.32 . 5 suy ra
log301350 = log30(30. 32. 5) = 1 + 2log303 + log305 = 1 + 2a + b.
b) log2515 = =
=
=
=
.
Tính :
a) \(\dfrac{1}{2}\log_736-\log_714-3\log_7\sqrt[3]{21}\)
b) \(\dfrac{\log_224-\dfrac{1}{2}\log_272}{\log_318-\dfrac{1}{3}\log_372}\)
c) \(\dfrac{\log_24+\log_2\sqrt{10}}{\log_220+3\log_22}\)
Tìm x, biết :
a) \(\log_5x=2\log_5a-3\log_5b\)
b) \(\log_{\dfrac{1}{2}}x=\dfrac{2}{3}\log_{\dfrac{1}{2}}a-\dfrac{1}{5}\log_{\dfrac{1}{2}}b\)
a) Cho \(a=\log_315;b=\log_310\). Hãy tính \(\log_{\sqrt{3}}50\) theo a, b ?
b) Cho \(a=\log_23;b=\log_35;c=\log_72\). Hãy tính \(\log_{140}63\) theo a, b, c ?
Hãy so sánh mỗi cặp số sau :
a) \(\log_3\dfrac{6}{5}\) và \(\log_3\dfrac{5}{6}\)
b) \(\log_{\dfrac{1}{3}}9\) và \(\log_{\dfrac{1}{3}}17\)
c) \(\log_{\dfrac{1}{2}}e\) và \(\log_{\dfrac{1}{2}}\pi\)
d) \(\log_2\dfrac{\sqrt{5}}{2}\) và \(\log_2\dfrac{\sqrt{3}}{2}\)
a) \(log_3\dfrac{6}{5}>log_3\dfrac{5}{6}\) vì \(\dfrac{6}{5}>\dfrac{5}{6}\)
b) \(log_{\dfrac{1}{3}}9>log_{\dfrac{1}{3}}17\) vì \(9>17\) và \(0< \dfrac{1}{3}< 1\).
c) \(log_{\dfrac{1}{2}}e>log_{\dfrac{1}{2}}\pi\) vì \(e>\pi\) và \(0< \dfrac{1}{2}< 1\)
d) \(log_2\dfrac{\sqrt{5}}{2}>log_2\dfrac{\sqrt{3}}{2}\) vì \(\dfrac{\sqrt{5}}{2}>\dfrac{\sqrt{3}}{2}\).
Trả lời bởi Nguyễn Đắc ĐịnhChứng minh rằng :
a) \(\log_{a_1}a_2.\log_{a_2}a_3.\log_{a_3}a_4.....\log_{a_{n-1}}a_n=\log_{a_1}a_n\)
b) \(\dfrac{1}{\log_ab}+\dfrac{1}{\log_{a^2}b}+\dfrac{1}{\log_{a^3}b}+.....+\dfrac{1}{\log_{a^nb}}=\dfrac{n\left(n+1\right)}{2\log_ab}\)
a) Áp dụng công thức: \(\log_ab.\log_bc=\log_ac\)
b) Vì \(\dfrac{1}{\log_{a^k}b}=\dfrac{1}{\dfrac{1}{k}\log_ab}=\dfrac{k}{\log_ab}\) nên biểu thức vế trái bằng:
\(VT=\dfrac{1}{\log_ab}\left(1+2+...+n\right)\)
\(=\dfrac{1}{\log_ab}.\dfrac{n\left(n+1\right)}{2}=VP\)
Trả lời bởi Giáo viên Toán
a)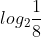
= 
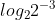= -3.
b)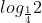
= 
= 
.
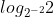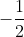hoặc dùng công thức đổi cơ số :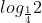
= 
= 
= 
.
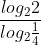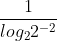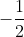c)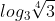
= 
= 
.
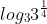d)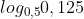
= 
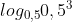= 3.
Trả lời bởi ¨°o.O♫♀¤♪ Zin Phan ♪¤♂♫O...