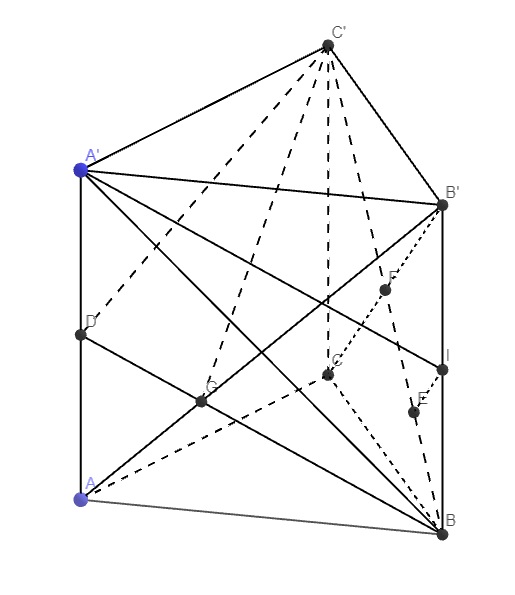
cho hình lăng trụ đứng ABC.A'B'C' có AB=a, AC=2a, AA'=\(\dfrac{3a\sqrt{6}}{2}\)và góc BAC = 60 độ. gọi M là điểm nằm trên cạnh CC' sao cho \(\overrightarrow{CM}=2\overrightarrow{MC'}\)
a, CMR AM vuông góc B'M
b, tính khoảng cánh từ A' đến mặt phẳng (AB'M)
cho khối chóp S.ABCD có đáy hình thang vuông tại A,B, biết AB=BC=2a, AD=a. Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách giữa SA và CD bằng 4a/5. tính thể tích S.ABCD
Gọi H là hình chiếu của S lên (ABCD)
\(\left\{{}\begin{matrix}CD\perp SH\\CD\perp SC\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHC\right)\Rightarrow CD\perp CH\)
\(SB=SC\Rightarrow HB=HC\Rightarrow H;M;D\) thẳng hàng với M là trung điểm CD
Tứ giác ADCM là hình bình hành (AD song song và bằng CM)
\(\Rightarrow CD||\left(SAM\right)\Rightarrow d\left(SA;CD\right)=d\left(CD;\left(SAM\right)\right)=d\left(D;\left(SAM\right)\right)\)
Hệ thức lượng trong tam giác vuông HCD với đường cao CM:
\(CM^2=HM.DM\Rightarrow HM=\dfrac{CM^2}{DM}=\dfrac{a^2}{2a}=\dfrac{a}{2}\)
\(\Rightarrow HM=\dfrac{1}{4}DM\Rightarrow d\left(H;\left(SAM\right)\right)=\dfrac{1}{4}d\left(D;\left(SAM\right)\right)=\dfrac{a}{5}\)
Kéo dài AM cắt HC tại E \(\Rightarrow AE\perp CH\) (do \(AE||CD\)) \(\Rightarrow AE\perp\left(SCH\right)\)
Từ H kẻ \(HF\perp SE\) (F thuộc SE)
\(\Rightarrow HF\perp\left(SAM\right)\Rightarrow HF=d\left(H;\left(SAM\right)\right)=\dfrac{a}{5}\)
\(CH^2=HM.HD=\dfrac{a}{2}\left(\dfrac{a}{2}+2a\right)=\dfrac{5a^2}{4}\Rightarrow CH=\dfrac{a\sqrt{5}}{2}\)
\(HM^2=HE.CH\Rightarrow HE=\dfrac{HM^2}{CH}=\dfrac{a\sqrt{5}}{10}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow SH=\dfrac{a\sqrt{5}}{5}\)
\(\Rightarrow V=...\)
cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a.
a, tính góc giữa AB' và mặt phẳng (ABC)
b, gọi G là trọng tâm tam giác AA'B, I la trung điểm BB'. Tính khoảng cách giữa C'G và A'I
a. Tam giác AA'B vuông cân tại A nên \(\widehat{A'BA}=45^0\)
b.
Gọi D là trung điểm AA'\(\Rightarrow D,B,G\) thẳng hàng
Tứ giác A'IBD là hình bình hành
\(\Rightarrow A'I||BD\Rightarrow A'I||\left(C'BD\right)\Rightarrow d\left(A'I;C'G\right)=d\left(A'I;\left(C'BD\right)\right)=d\left(I;\left(C'BD\right)\right)\)
Gọi F là giao điểm B'C và BC'
Ta có \(DC'=DB=\dfrac{a\sqrt{5}}{2}\) (pitago) \(\Rightarrow\Delta BDC'\) cân tại B
\(\Rightarrow DF\perp BC'\)
Tương tự, \(\Delta CDB'\) cân tại D \(\Rightarrow DF\perp B'C\)
\(\Rightarrow DF\perp\left(BCC'B'\right)\Rightarrow\left(C'BD\right)\perp\left(BCC'B'\right)\)
Từ I kẻ \(IE\perp BC'\Rightarrow IE\perp\left(C'BD\right)\Rightarrow IE=d\left(I;\left(C'BD\right)\right)\)
\(IE=\dfrac{1}{2}B'F=\dfrac{a\sqrt{2}}{4}\) (đường trung bình)
\(\Rightarrow d\left(C'G;A'I\right)=\dfrac{a\sqrt{2}}{4}\)
1) Cho hinh chop tam giac deu S.ABC co dien tich day bang 2\(\sqrt{3}\) va dien tich mot mat ben bang 4. The tich khoi chop S.ABC bang:
Cho hình chóp SABCD. Có SA \(\perp\)đáy. ABCD là hình chữ nhật có AB = \(a\sqrt{7}\), AD = \(a\sqrt{2}\), SC = \(2\sqrt{2a}\). Tính thể tích \(V_{SABCD}\)
\(AC=\sqrt{AB^2+AD^2}=3a\)
\(SA=\sqrt{8a^2-9a^2}=\sqrt{-a^2}\)
=>Đề sai rồi bạn
cho hình chóp S.ABC có SA vuônh góc với (ABC), SA =a, tam giac ABC vuông cân tại A cạnh BC =2acăn(2) a. Vs.abc ? b. trên SA,SB,SC lấy M,N,P sao cho SM=3MA; SN=4NB; SP=5PC. tính Vmnpabc
a. Tam giác ABC vuông cân tại A....Suy ra AB=AC=2a
\(Vs.abc=\dfrac{1}{3}.SA.S_{\Delta ABC}=\dfrac{1}{3}.a.\dfrac{1}{2}.2a.2a=\dfrac{2}{3}a^3\)
b. Tính S khối chóp bằng phương pháp tỉ số thể tích
Cho h/c S.ABC có mp \(\left(\alpha\right)\) không qua S cắt SA,SB,SC tại A',B',C', khi đó:
\(\dfrac{V_{S.A'B'C'}}{V_{S.ABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}\)
Cm: Kẻ C'H' , CH lần lượt vuông góc với SB', SB
\(\Rightarrow\dfrac{S_{SB'C'}}{S_{SBC}}=\dfrac{\dfrac{1}{2}.C'H'.SB'}{\dfrac{1}{2}CH.SB}=\dfrac{SC'}{SC}.\dfrac{SB'}{SB}\)
\(\dfrac{V_{S.A'B'C'}}{V_{S.ABC}}=\dfrac{S_{SB'C'}.d\left(A',\left(SB'C'\right)\right)}{S_{SBC}.d\left(A,\left(SBC\right)\right)}\)
\(=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}\)
Áp dụng: \(\dfrac{V_{SMNP}}{V_{SABC}}=\dfrac{3}{4}.\dfrac{4}{5}.\dfrac{5}{6}=\dfrac{1}{2}\)
\(\Rightarrow V_{MNPABC}=V_{SABC}-V_{SMNP}=\dfrac{1}{2}V_{SABC}=\dfrac{1}{3}a^3\)
Hộ mình với ạ 
Ta có :
$SA ⊥ BC$ ; $AB ⊥ BC$ suy ra $BC ⊥ (SAB)$
Do đó $(SC;(SAB)) = ∠BSC = 60^o$
Tam giác ABC vuông cân tại B nên ta có :
$BA^2 + BC^2 = AC^2 = 2a^2 \Rightarrow BA = BC = a$
Ta có : $SC.sin(BSC) = BC \Rightarrow SC = \dfrac{a}{sin(60^o)}$ = \(\dfrac{2\sqrt{3}}{3}\)a
$SA^2 + AC^2 = SC^2 \Rightarrow SA = $\(\dfrac{\sqrt{3}}{3}\)a
Vậy, \(V_{S.ABC}=\dfrac{1}{3}.\dfrac{\sqrt{3}}{3}a.\dfrac{1}{2}.a.a=\dfrac{\sqrt{3}}{18}a^3\)
giup mình vouw ạ
