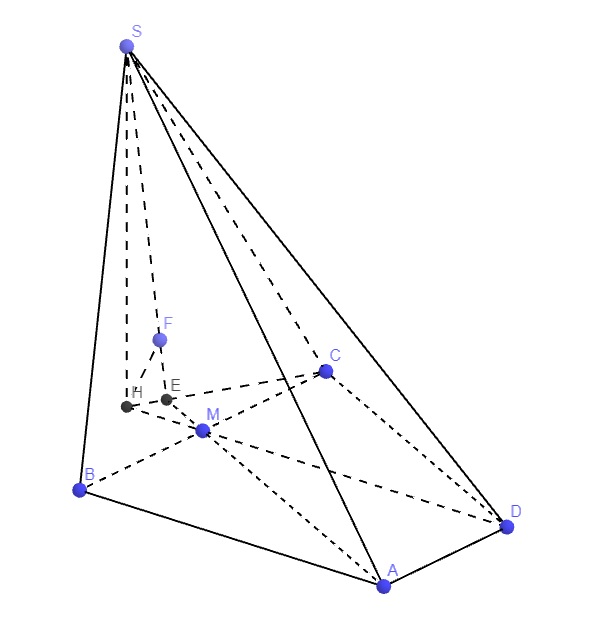
Gọi H là hình chiếu của S lên (ABCD)
\(\left\{{}\begin{matrix}CD\perp SH\\CD\perp SC\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHC\right)\Rightarrow CD\perp CH\)
\(SB=SC\Rightarrow HB=HC\Rightarrow H;M;D\) thẳng hàng với M là trung điểm CD
Tứ giác ADCM là hình bình hành (AD song song và bằng CM)
\(\Rightarrow CD||\left(SAM\right)\Rightarrow d\left(SA;CD\right)=d\left(CD;\left(SAM\right)\right)=d\left(D;\left(SAM\right)\right)\)
Hệ thức lượng trong tam giác vuông HCD với đường cao CM:
\(CM^2=HM.DM\Rightarrow HM=\dfrac{CM^2}{DM}=\dfrac{a^2}{2a}=\dfrac{a}{2}\)
\(\Rightarrow HM=\dfrac{1}{4}DM\Rightarrow d\left(H;\left(SAM\right)\right)=\dfrac{1}{4}d\left(D;\left(SAM\right)\right)=\dfrac{a}{5}\)
Kéo dài AM cắt HC tại E \(\Rightarrow AE\perp CH\) (do \(AE||CD\)) \(\Rightarrow AE\perp\left(SCH\right)\)
Từ H kẻ \(HF\perp SE\) (F thuộc SE)
\(\Rightarrow HF\perp\left(SAM\right)\Rightarrow HF=d\left(H;\left(SAM\right)\right)=\dfrac{a}{5}\)
\(CH^2=HM.HD=\dfrac{a}{2}\left(\dfrac{a}{2}+2a\right)=\dfrac{5a^2}{4}\Rightarrow CH=\dfrac{a\sqrt{5}}{2}\)
\(HM^2=HE.CH\Rightarrow HE=\dfrac{HM^2}{CH}=\dfrac{a\sqrt{5}}{10}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow SH=\dfrac{a\sqrt{5}}{5}\)
\(\Rightarrow V=...\)