Bài 2: Khối đa diện lồi và khối đa diện đều
Nội dung lý thuyết
Các phiên bản khácI. KHỐI ĐA DIỆN LỒI
Khối đa diện \(\left(H\right)\) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của \(\left(H\right)\) luôn thuộc \(\left(H\right)\). Khi đó đa diện xác định \(\left(H\right)\) được gọi là đa diện lồi.
Ví dụ: Các khối lăng trụ tam giác, khối hộp, khối tứ diện,... đều là các khối đa diện lồi.
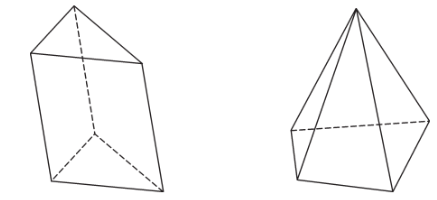
Nhận xét: Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng chứa một mặt của nó.
II. KHỐI ĐA DIỆN ĐỀU
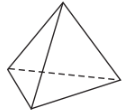
Đối với khối tứ diện đều, các mặt của nó là những tam giác đều, mỗi đỉnh của nó là đỉnh chung của đúng ba mặt.
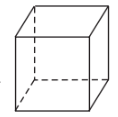
Đối với khối lập phương, các mặt của nó là các hình vuông, mỗi đỉnh của nó là đỉnh chung của ba mặt.
Định nghĩa:
Khối đa diện đều là khối đa diện lồi có các tính chất sau:
a) Mỗi mặt của nó là một đa giác đều \(p\) cạnh ;
b) Mỗi đỉnh của nó là đỉnh chung của đúng \(q\) mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại \(\left\{p;q\right\}\).
Nhận xét: Các mặt của khối đa diện đều là các đa giác đều bằng nhau.
Định lí:
Chỉ có \(5\) loại đa diện đều. Đó là loại \(\left\{3;3\right\}\), loại \(\left\{4;3\right\}\), loại \(\left\{3;4\right\}\), loại \(\left\{5;3\right\}\) và loại \(\left\{3;5\right\}\).
@2442145@
Năm loại khối đa diện đều kể trên theo thứ tự được gọi là khối tứ diện đều, khối lập phương, khối bát diện đều, khối mười hai mặt đều và và khối hai mươi mặt đều.

| Loại | Tên gọi | Số đỉnh | Số cạnh | Số mặt |
| \(\left\{3;3\right\}\) | Tứ diện đều | 4 | 6 | 4 |
| \(\left\{4;3\right\}\) | Lập phương | 8 | 12 | 6 |
| \(\left\{3;4\right\}\) | Bát diện đều | 6 | 12 | 8 |
| \(\left\{5;3\right\}\) | Mười hai mặt đều | 20 | 30 | 12 |
| \(\left\{3;5\right\}\) | Hai mươi mặt đều | 12 | 30 | 12 |
@2440893@@2440950@