
mọi người giúp mình với

mọi người giúp mình với
Hai đường thẳng đã cho song song khi:
\(\left\{{}\begin{matrix}m-1=-2\\m+3\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m\ne-2\end{matrix}\right.\)
\(\Rightarrow m=-1\) (không thỏa mãn điều kiện đề bài)
Vậy không tồn tại m để 2 đường thẳng đã cho song song
Trong mặt tọa độ xOy, chp parabol \(\left(P\right):y=ax^2\) qua \(M\left(\sqrt{3};3\right)\) và đường thẳng \(\left(d\right):y=\dfrac{1}{2}x+m\) (m là tham số). Xác định phương trình Parabol (P) từ đó tìm tất cả giá trị của tham số m để (d) cắt (P) tại Hai điểm phân biệt \(A\left(x_A;y_A\right)\) ; \(B\left(x_B;y_B\right)\) khác gốc tọa độ sao cho \(\dfrac{y_A}{x_B}+\dfrac{y_B}{x_A}=\dfrac{25}{16}\)
Thay `M(\sqrt{3};3)` vào `(P)` có: `3=a(\sqrt{3})^2<=>a=1`
`=>(P):y=x^2`
Hoành độ giao điểm của `(P)` và `(d)` là: `1/2x+m=x^2`
`<=>2x^2-x-2m=0` `(1)`
`(d)` cắt `(P)` tại `2` điểm phân biệt `<=>` Ptr `(1)` có `2` ngiệm pb
`<=>\Delta > 0`
`<=>(-1)^2-2(-2m) > 0`
`<=>1+4m > 0<=>m > -1/4`
Với `m > -1/4` áp dụng Viét có: `{(x_A+x_B=[-b]/a=1/2),(x_A.x_B=c/a=-m):}`
Vì `A(x_A;y_A)` và `B(x_B;y_B) in (P)=>{(y_A=x_A ^2),(y_B=x_B ^2):}`
Có: `[y_A]/[x_B]+[y_B]/[x_A]=25/16`
`<=>[x_A ^2]/[x_B]+[x_B ^2]/[x_A]=25/16`
`<=>[x_A ^3+x_B ^3]/[x_A .x_B]=25/16`
`<=>[(x_A+x_B)[(x_A+x_B)^2-3x_A .x_B]]/[x_A .x_B]=25/16`
`<=>[1/2[(1/2)^2+3m]]/[-m]=25/16`
`<=>8(1/4+3m)=-25m`
`<=>2+24m=-25m`
`<=>m=-2/49`
P/s: Mk xin phép gỡ CHH, câu này cũng ko nhất thiết phải đưa lên CHH đâu bạn!

mọi người giúp mình với
b) \(d\cap Oy=\left(0;3\right)\)
\(d\cap Ox=>y=0=>x=\dfrac{3}{4}=>\left(\dfrac{3}{4};0\right)\)
c) \(d_{\left(0;d\right)}=\dfrac{\left|3\right|}{\sqrt{1^2+4^2}}=\dfrac{3}{\sqrt{17}}\)
d) \(d_{\left(x;d\right)}=\dfrac{\left|4.\left(-1\right)+\left(-2\right).1-3\right|}{\sqrt{4^2+1^2}}=\dfrac{9}{\sqrt{17}}\)
e) \(S_{OAB}=\dfrac{1}{2}.\dfrac{3}{4}.3=\dfrac{9}{8}\)
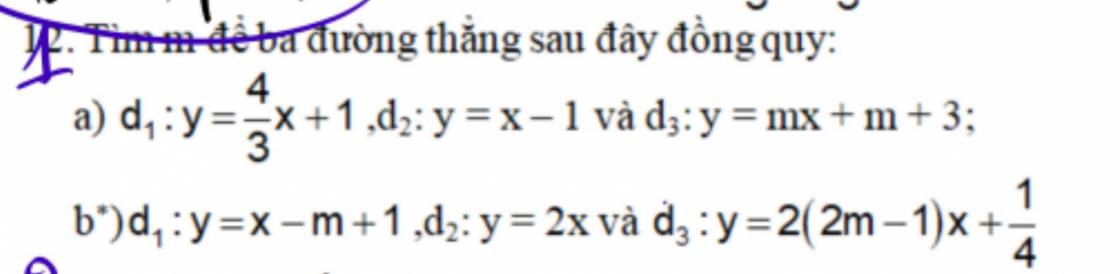
mọi người giúp mình với ạ
a) PT hoành độ giao điểm của \(d_1\)và \(d_2\) là
\(\dfrac{4}{3}x+1=x-1< =>\dfrac{1}{3}x=-2< =>x=-6\)
\(=>y=-6-1=-7\)
Để \(d_1;d_2;d_3\) đồng quy thì \(d_3\) đi qua \(\left(-6;-7\right)=>-7=m.\left(-6\right)+m+3< =>-5m=-10< =>m=2\)
Vậy \(m=2\)
b) PT hoành độ giao điểm của \(d_1\)và \(d_2\) là
\(x-m+1=2x< =>x=1-m=>y=2.\left(1-m\right)=2-2m\)
Để \(d_1;d_2;d_3\) đồng quy thì \(d_3\) đi qua \(\left(1-m;2-2m\right)\)
\(=>2-2m=2\left(2m-1\right)\left(1-m\right)+\dfrac{1}{4}\)
\(< =>2-2m=-4m^2+6m-2+\dfrac{1}{4}\)
\(< =>-4m^2+8m-\dfrac{15}{4}=0\)
\(< =>\dfrac{-1}{4}\left(4m-3\right)\left(5-4m\right)=0\)
\(< =>\left[{}\begin{matrix}4m-3=0\\5-4m=0\end{matrix}\right.< =>\left[{}\begin{matrix}m=\dfrac{3}{4}\\m=\dfrac{5}{4}\end{matrix}\right.\)
Với \(m=\dfrac{3}{4}=>\left\{{}\begin{matrix}\left(d_1\right):y=x+\dfrac{1}{4}\\\left(d_3\right):y=x+\dfrac{1}{4}\end{matrix}\right.=>d_1\equiv d_3\) (loại)
Vậy \(m=\dfrac{5}{4}\)
Cho hàm số y = -x² và (d) : y = x-2 a) vẽ (P) và (d) b) Tìm M ∈ (P) có hoành độ lớn hơn -2 và nhỏ hơn 1. Đồng thời khoảng cách từ M đến (d) là lớn nhất
viết phương trình đường thẳng (d) đi qua hai điểm A,B nằm trên (P) có hoành độ lần lượt là -1;2
Cho hàm số y=1/2 x^2(P)
Và. y=x+3/2(d)
A)Vẽ đt P và d
B)Tìm giao điểm của P và d
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2-x-\dfrac{3}{2}=0\)
\(\Leftrightarrow x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
KHi x=3 thì \(y=\dfrac{1}{2}x^2=\dfrac{9}{2}\)
Khi x=-1 thì \(y=\dfrac{1}{2}x^2=\dfrac{1}{2}\)
cho đường thẳng (d) : y=mx+m+1 và parabol (P) : y=x^2 . Tìm m để (d) cắt (P) tại hai điểm có hoành độ x1,x2 nằm khác phía đối vs trục tung thỏa mãn điều kiện : 2x1-3x2=5
Hoành độ của 2 giao điểm là nghiệm của phương trình
⇒⎧⎪ ⎪⎨⎪ ⎪⎩x1=5m−2m+55=3m+55x2=2m−55⇒{x1=5m−2m+55=3m+55x2=2m−55
Thay
Cho các đường thẳng (d1): y= (m2+1)x +m và (d2): y=5x+2. Tìm m để hai đường thẳng song song
`(d1) //// (d2) <=> {(a = a'),(b \ne b'):}`
`<=>{(m^2 + 1 = 5),(1 \ne 2\text{ (Luôn đúng)}):}`
`<=> m^2 = 4`
`<=>m = +-2`
Vậy `m = +-2` thì `(d1) //// (d2)`
TK
(d1)//(d2)⇔{a=a'b≠b'(d1)//(d2)⇔{a=a′b≠b′
⇔{m2+1=51≠2 (Luôn đúng)⇔{m2+1=51≠2 (Luôn đúng)
⇔m2=4⇔m2=4
⇔m=±2⇔m=±2
Vậy m=±2m=±2 thì (d1)//(d2)
cho hàm số y = -2x^2 (1)
a) với giá trị nào của x thì hàm số (1) đồng biến
b) tìm tọa độ giao điểm của ddg thẳng y = -3x -5 với đths (1)
a.
Do \(a=-2< 0\Rightarrow\)hàm số (1) đồng biến khi \(x< 0\)
b.
Phương trình hoành độ giao điểm:
\(-2x^2=-3x-5\Leftrightarrow2x^2-3x-5=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\Rightarrow y=-2\\x=\dfrac{5}{2}\Rightarrow y=-\dfrac{25}{2}\end{matrix}\right.\)
Hai đồ thị cắt nhau tại 2 điểm có tọa độ: \(\left(-1;-2\right)\) và \(\left(\dfrac{5}{2};-\dfrac{25}{2}\right)\)