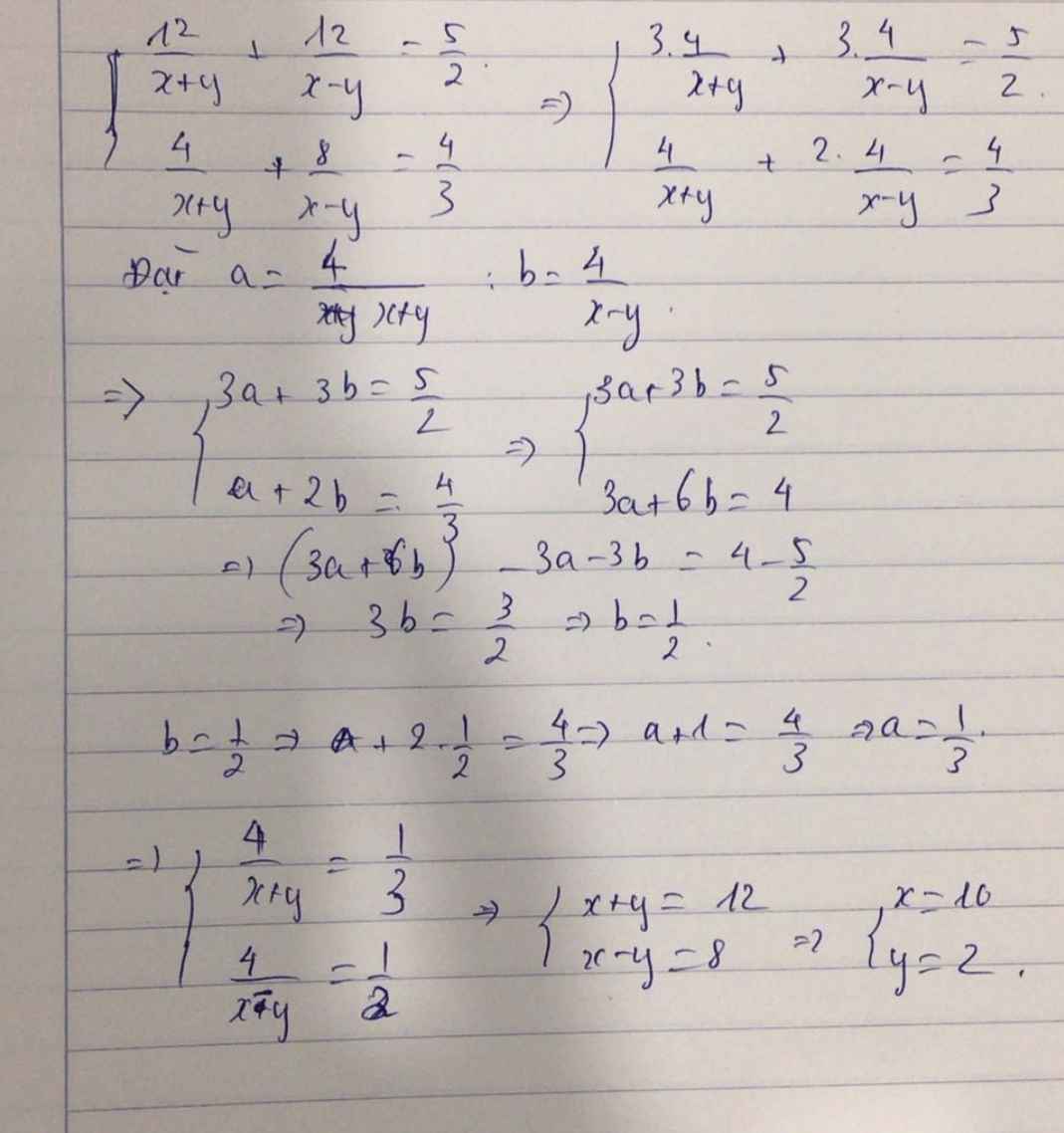Bài 1: Phương trình bậc nhất hai ẩn

ĐKXĐ: \(\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\y\ge-\dfrac{1}{3}\end{matrix}\right.\)

Ta có: \(4\sqrt{3y+1}=2.2.\sqrt{3y+1}\le2^2+3y+1=3y+5\)

\(\Rightarrow x^2+7\le3y+5\Rightarrow x^2-3y+2\le0\) (1)

Lại có: \(2\sqrt{3x-2}=2.1.\sqrt{3x-2}\le1^2+3x-2=3x-1\)

\(\Rightarrow y^2+xy\le3x-1\Rightarrow y^2+xy-3x+1\le0\) (2)

Cộng vế (1) và (2):

\(\Rightarrow x^2+xy+y^2-3x-3y+3\le0\)

\(\Rightarrow\left(x^2+\dfrac{y^2}{4}+\dfrac{9}{4}+xy-3x-\dfrac{3y}{2}\right)+\dfrac{3}{4}\left(y^2-2y+1\right)\le0\)

\(\Rightarrow\left(x+\dfrac{y}{2}-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\left(y-1\right)^2\le0\)

\(\Rightarrow\left\{{}\begin{matrix}x+\dfrac{y}{2}-\dfrac{3}{2}=0\\y-1=0\end{matrix}\right.\) \(\Rightarrow x=y=1\)

Thay vào hệ thấy thỏa mãn, vậy hệ có nghiệm duy nhất \(\left(x;y\right)=\left(1;1\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3.4}{x+y}+\dfrac{3.4}{x-y}=\dfrac{5}{2}\\\dfrac{4}{x+y}+\dfrac{2.4}{x+y}=\dfrac{4}{3}\end{matrix}\right.\\ Đặt.a=\dfrac{4}{x+y},b=\dfrac{4}{x-y}\\ \Leftrightarrow\left\{{}\begin{matrix}3a+3b=\dfrac{5}{2}\\a+2b=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=\dfrac{5}{2}\\3a+6b=4\end{matrix}\right.\) 

\(\Leftrightarrow\left(3a+6b\right)-3a-3b=4-\dfrac{5}{2}\\ \Leftrightarrow3b=\dfrac{3}{2}\Rightarrow b=\dfrac{1}{2}\Rightarrow a+2.\dfrac{1}{2}=\dfrac{4}{3}\\\Leftrightarrow a+1=\dfrac{4}{3}\Rightarrow a=\dfrac{1}{3}\\ \Rightarrow\left\{{}\begin{matrix}\dfrac{4}{x+y}=\dfrac{1}{3}\\\dfrac{4}{x+y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=12\\x-y=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=10\\y=2\end{matrix}\right.\)

Gọi số đó có dạng \(\overline{xy}=10x+y\) với x;y là các số tự nhiên từ 1 tới 9

Do số đó gấp 4 lần tổng các chữ số của nó nên ta có:

\(10x+y=4\left(x+y\right)\Rightarrow2x-y=0\)

Khi viết ngược số đó ta được số mới có giá trị là: \(10y+x\)

Do số mới lớn hơn số ban đầu 36 đơn vị nên:

\(10y+x-\left(10x+y\right)=36\Rightarrow y-x=4\)

Ta được hệ: \(\left\{{}\begin{matrix}2x-y=0\\y-x=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=8\end{matrix}\right.\)

Vậy số đó là 48

Gọi phương trình bậc nhất hai ẩn cần tìm là \(ax+by=0\)

Theo đề, ta có:

\(\left\{{}\begin{matrix}a+2b=0\\2a+5b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+4b=0\\2a+5b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=0\end{matrix}\right.\)

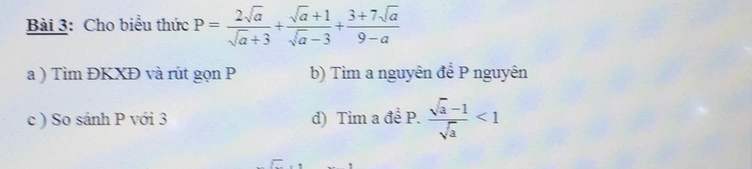
a, đkxđ : a >= 0 ; a khác 9 

\(P=\dfrac{2\sqrt{a}\left(\sqrt{a}-3\right)+\left(\sqrt{a}+1\right)\left(\sqrt{a}+3\right)-3-7\sqrt{a}}{a-9}\)

\(=\dfrac{2a-6\sqrt{a}+a+4\sqrt{a}+3-3-7\sqrt{a}}{a-9}=\dfrac{3a-9\sqrt{a}}{a-9}=\dfrac{3\sqrt{a}}{\sqrt{a}+3}\)

b, \(\dfrac{3\sqrt{a}}{\sqrt{a}+3}=\dfrac{3\left(\sqrt{a}+3\right)-9}{\sqrt{a}+3}=3-\dfrac{9}{\sqrt{a}+3}\Rightarrow\sqrt{a}+3\inƯ\left(9\right)=\left\{1;3;9\right\}\)

c, Ta có : \(3=\dfrac{3\left(\sqrt{a}+3\right)}{\sqrt{a}+3}\)mà \(3\left(\sqrt{a}+3\right)>3\sqrt{a}\)

Vậy P < 3 

d, Ta có : \(\dfrac{3\sqrt{a}}{\sqrt{a}+3}.\dfrac{\sqrt{a}-1}{\sqrt{a}}< 1\Leftrightarrow\dfrac{3\left(\sqrt{a}-1\right)}{\sqrt{a}+3}-1< 0\)

\(\Leftrightarrow\dfrac{3\sqrt{a}-3-\sqrt{a}-6}{\sqrt{a}+3}< 0\Rightarrow2\sqrt{a}-9< 0\)vì \(\sqrt{a}+3>0\)

\(\Leftrightarrow\sqrt{a}< \dfrac{9}{2}\Leftrightarrow a< \dfrac{81}{4}\)

Kết hợp đk vậy \(0\le a< \dfrac{81}{4}\)

Gọi số có 2 chữ số cần tìm là \(\overline{ab}\left(0< a< 10;0< b< 10\right)\)

Vì 2 lần chữ số hàng chục lớn hơn 3 lần chữ số đơn vị là 2

=> PT : 2a - 3b = 2 (1)

Lại có khi viết ngược lại số mới nhỏ hơn số ban đầu 18 đơn vị 

=> PT : \(\overline{ab}-\overline{ba}=18\)

<=> a - b = 2 (2)

Từ (1)(2) => HPT : \(\left\{{}\begin{matrix}2a-3b=2\\a-b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\left(b+2\right)-3b=2\\a=b+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2\\a=4\end{matrix}\right.\)

Vậy số cần tìm là 42

b) (0,5 - x)² - 3 = 0 ⇔ 0,5² + x² - 2.0,5x - 3 = 0

                               ⇔ x² + 0,25 - x - 3 = 0

                               ⇔ x² - x - 2,75 = 0

                               ⇔ ????

c: \(\Leftrightarrow\left(2x-3\sqrt{2}\right)\left(2x+\sqrt{2}\right)=0\)

hay \(x\in\left\{\dfrac{3\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right\}\)

Lời giải:
Hai đường thẳng $y=ax+b$ và $y=a'x+b'$ cắt nhau khi $a\neq a'$