Bài 1: Phương trình bậc nhất hai ẩn

a: Khi m=1 thì phương trình sẽ là \(5x^2-3x+1-1=0\)

=>\(5x^2-3x=0\)

=>x(5x-3)=0

=>\(\left[{}\begin{matrix}x=0\\x=\dfrac{3}{5}\end{matrix}\right.\)

b: \(\Delta=\left(-3\right)^2-4\cdot5\cdot\left(m-1\right)\)

=9-20(m-1)

=9-20m+20

=-20m+29

Để phương trình có hai nghiệm thì Δ>=0

=>-20m+29>=0

=>-20m>=-29

=>\(m< =\dfrac{29}{20}\)

c: Để phương trình có hai nghiệm phân biệt thì Δ>0

=>-20m+29>0

=>-20m>-29

=>\(m< \dfrac{29}{20}\)

d: Để phương trình có nghiệm kép thì Δ=0

=>-20m+29=0

=>-20m=-29

=>m=1,45

Để phương trình vô nghiệm thì Δ<0

=>-20m+29<0

=>-20m<-29

=>m>1,45

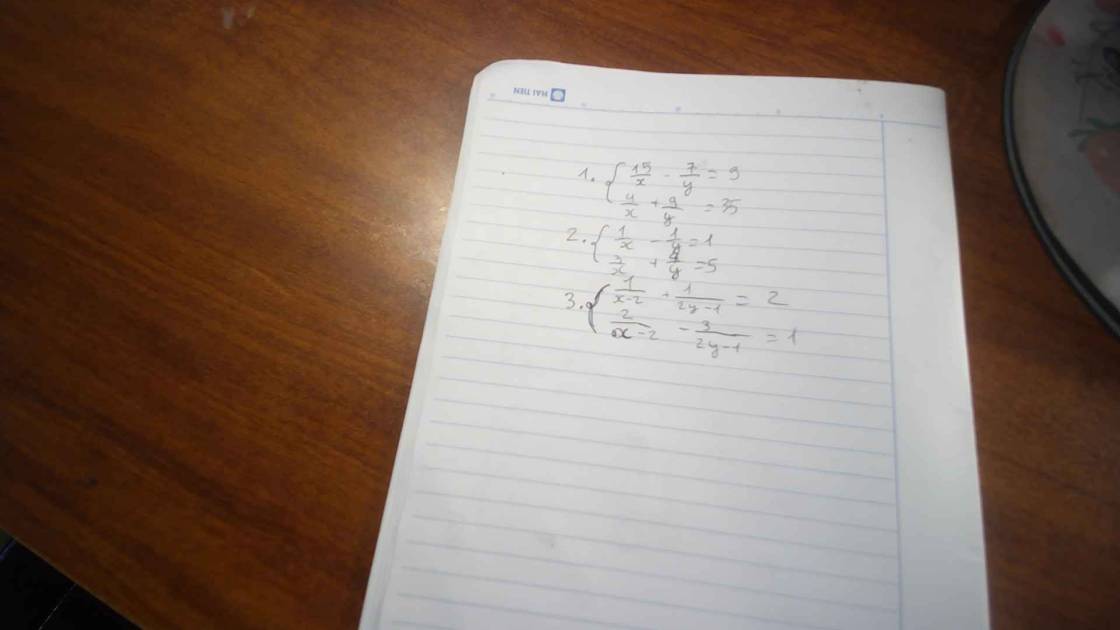
1.

ĐKXĐ: \(x\ne0;y\ne0\)

Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=u\\\dfrac{1}{y}=v\end{matrix}\right.\) ta được:

\(\left\{{}\begin{matrix}15u-7v=9\\4u+9v=35\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}135u-63v=81\\28u+63v=245\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}163u=326\\4u+9v=35\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u=2\\v=\dfrac{35-4u}{9}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u=2\\v=3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=2\\\dfrac{1}{y}=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)

2.

ĐKXĐ: \(x\ne0;y\ne0\)

Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=u\\\dfrac{1}{y}=v\end{matrix}\right.\) ta được hệ:

\(\left\{{}\begin{matrix}u-v=1\\3u+4v=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4u-4v=4\\3u+4v=5\\\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}7u=9\\3u+4v=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{9}{7}\\v=\dfrac{5-3u}{4}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{9}{7}\\v=\dfrac{2}{7}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{9}{7}\\\dfrac{1}{y}=\dfrac{2}{7}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{7}{9}\\y=\dfrac{7}{2}\end{matrix}\right.\)

Chụp gần lại em, hình mờ quá ko nhìn thấy gì

Lời giải:
Gọi chiều dài và chiều rộng của hình chữ nhật là $a,b$ (m) 

Theo bài ra ta có:

$a+b=134:2=67$ 

$(a-1)(b-1)=28^2=784$

$\Leftrightarrow ab-(a+b)+1=784$

$\Leftrightarrow ab-67+1=784$

$\Leftrightarrow ab=850$

Từ $a+b=67$ và $ab=850$ áp dụng định lý Viet đảo thì:

$a,b$ là nghiệm của pt:

$X^2-67X+850=0$

$\Rightarrow (a,b) = (50,17)$

Mà $a>b$ nên chiều dài là 50 m, chiều rộng là 17m 

Bài nào em hỉ?

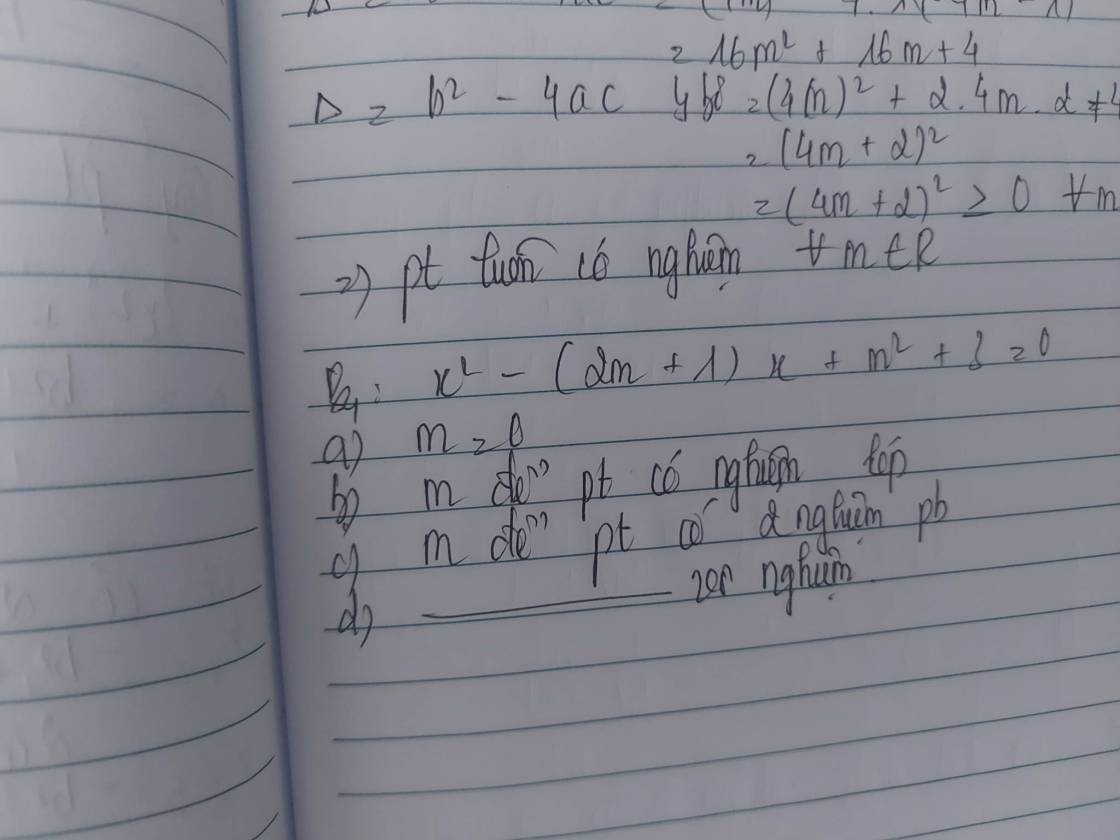
`a)m=0=>x^2-x+3=0<=>(x-1/2)^2+11/4=0` (Vô lí)

  `=>m=0` ptr vô nghiệm

`b)` Ptr có nghiệm kép `<=>\Delta=0`

  `<=>[-(2m+1)]^2-4(m^2+3)=0`

  `<=>4m^2+4m+1-4m^2-12=0`

  `<=>4m-11=0`

  `<=>m=11/4`

`c)` Ptr có `2` nghiệm pb`<=>\Delta > 0`

                                       `<=>4m-11 > 0<=>m > 11/4`

`d)` Ptr vô nghiệm `<=>\Delta < 0<=>4m-11 < 0<=>m < 11/4`

Bài 2:

a: Khi m=0 thì pt sẽ là:

\(x^2-x+3=0\)

=>\(x\in\varnothing\)

b: \(\Delta=\left(2m+1\right)^2-4\left(m^2+3\right)\)

=4m^2+4m+1-4m^2-12

=4m-11

Để pt có nghiệm kép thì 4m-11=0

=>m=11/4

c: Để phương trình có hai nghiệm pb thì 4m-11>0

=>m>11/4

d: Để pt vô nghiệm thì 4m-11<0

=>m<11/4

Phương trình đã cho có vô số nghiệm

Một cặp nghiệm của pt là \(\left(x;y\right)=\left(0;-2\right)\)

a: 0x+y=1

b: 3x+8y=12

c: x+0y=-2