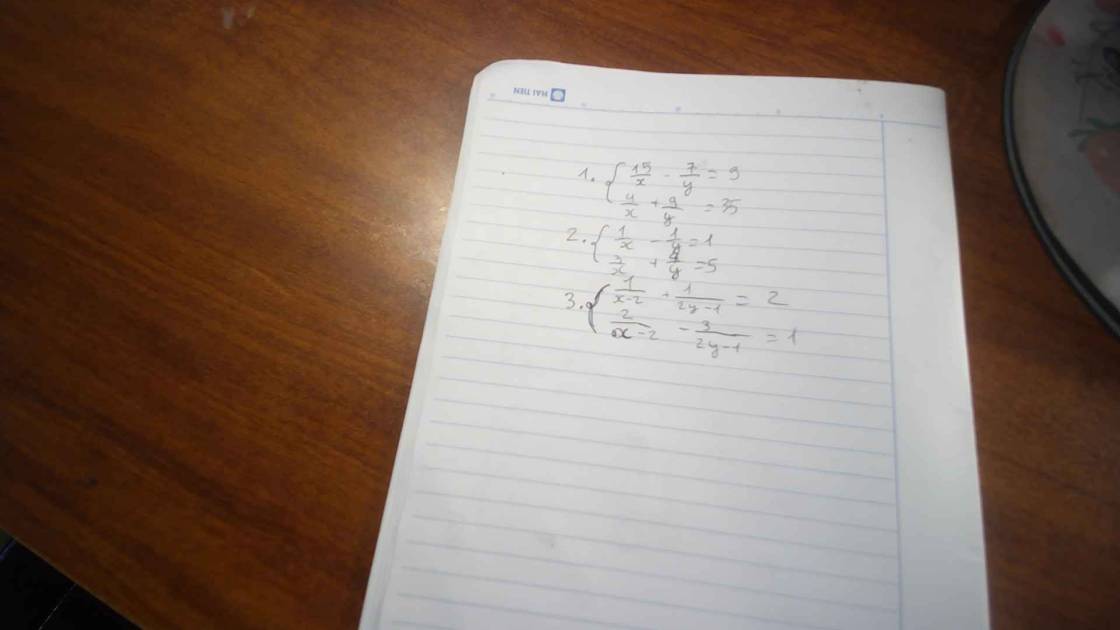Question

cứu

Answer 1

1.

ĐKXĐ: \(x\ne0;y\ne0\)

Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=u\\\dfrac{1}{y}=v\end{matrix}\right.\) ta được:

\(\left\{{}\begin{matrix}15u-7v=9\\4u+9v=35\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}135u-63v=81\\28u+63v=245\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}163u=326\\4u+9v=35\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u=2\\v=\dfrac{35-4u}{9}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u=2\\v=3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=2\\\dfrac{1}{y}=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)

Answer 2

2.

ĐKXĐ: \(x\ne0;y\ne0\)

Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=u\\\dfrac{1}{y}=v\end{matrix}\right.\) ta được hệ:

\(\left\{{}\begin{matrix}u-v=1\\3u+4v=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4u-4v=4\\3u+4v=5\\\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}7u=9\\3u+4v=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{9}{7}\\v=\dfrac{5-3u}{4}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{9}{7}\\v=\dfrac{2}{7}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{9}{7}\\\dfrac{1}{y}=\dfrac{2}{7}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{7}{9}\\y=\dfrac{7}{2}\end{matrix}\right.\)

Answer 3

Chụp gần lại em, hình mờ quá ko nhìn thấy gì

Answer 4

3.

ĐKXĐ: \(x\ne2;y\ne\dfrac{1}{2}\)

Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x-2}=u\\\dfrac{1}{2y-1}=v\end{matrix}\right.\) ta được:

\(\left\{{}\begin{matrix}u+v=2\\2u-3v=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3u+3v=6\\2u-3v=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}5u=7\\2u-3v=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{7}{5}\\v=\dfrac{2u-1}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{7}{5}\\v=\dfrac{3}{5}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x-2}=\dfrac{7}{5}\\\dfrac{1}{2y-1}=\dfrac{3}{5}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x-2=\dfrac{5}{7}\\2y-1=\dfrac{5}{3}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{19}{7}\\y=\dfrac{4}{3}\end{matrix}\right.\)