Cho tam giác ABC cân tại A. Qua B kẻ đường thẳng vuông góc với AB, qua C kẻ đường thẳng vuông góc với AC, chúng cắt nhau tại D. Chứng minh rằng AD là tia phân giác của góc A ?
Tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A.
Chứng minh rằng tam giác ABC là tam giác cân ?
Vì M là trung điểm của BC
=> BM = MC
Xét \(\Delta ABM\)và \(\Delta ACM\) có:
\(\widehat{BAM}=\widehat{CAM}\) ( AM là tia phân giác \(\widehat{A}\) )
AM (chung)
BM = CM (cmt)
Do đó: \(\Delta ABM=\Delta ACM\left(c-g-c\right)\)
=> AB = AC (hai cạnh tương ứng)
=> \(\Delta ABC\) cân tại A
Trả lời bởi Lê Vương Kim Anh
Cho tam giác ABC cân tại A. Kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A ?
C1: Xét \(\Delta ABD\) và \(\Delta ACD\) có:
AD (chung)
\(\widehat{ADB}=\widehat{ADC}\) ( = 900)
AB = AC ( \(\Delta ABC\)cân tại A )
Do đó: \(\Delta ABD=\Delta ACD\) (cạnh huyền - cạnh góc vuông)
Trả lời bởi Lê Vương Kim AnhCho tam giác ABC cân tại A. Các đường trung trực của AB, AC cắt nhau ở I. Chứng minh rằng AI là tia phân giác của góc A ?
Gọi M, N là trung điểm của AB, AC
Xét hai tam giác vuông AMI và ANI có:
AI: cạnh huyền chung
AM = AN (gt)
Vậy: \(\Delta AMI=\Delta ANI\left(ch-cgv\right)\)
Suy ra: \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
Do đó: AI là tia phân giác của góc A.
Trả lời bởi Hải NgânCho tam giác ABC cân tại A. Kẻ BD vuông góc với AC, kẻ CE vuông góc với AB. Gọi K là giao điểm của BD và CE. Chứng minh AK là tia phân giác của góc A ?
Xét hai tam giác ADB và AEC có:
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{A}\): góc chung
Vậy: \(\Delta ADB=\Delta AEC\left(ch-gn\right)\)
Suy ra: AD = AE (hai cạnh tương ứng)
Xét hai tam giác vuông ADK và AEK có:
AK: cạnh huyền chung
AD = AE (cmt)
Vậy: \(\Delta ADK=\Delta AEK\left(ch-cgv\right)\)
Suy ra: \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
Do đó: AK là tia phân giác của góc A.
Trả lời bởi Hải NgânTìm tam giác bằng nhau trên hình 148 :
Ta có: ∆AMD=∆AME(Cạnh huyền AM chung, góc nhọn^A1 = ^A2)
∆MDB=∆MEC(Cạnh huyền BM=CM, cạnh góc vuông.
MD=ME, do ∆AMD=∆AME)
∆AMB= ∆AMC(Cạnh AM chung),
Cạnh MB=MC, cạnh AB=AC
Vì AD=AE, DB=EC
Các tam giác vuông ABC và DEF có \(\widehat{A}=\widehat{D}=90^0\). AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau (về cạnh hay về góc) để \(\Delta ABC=\Delta DEF\) ?
Bổ sung thêm AB=DE
Thì ∆ABC=∆DEF (c.g.c)
* Bổ sung thêm ˆCC^=ˆFF^
Thì ∆ABC=∆DEF(g.c.g)
* Bổ sung thêm BC=EF
thì ∆ABC=∆DEF (cạnh huyền- cạnh góc vuông)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC \(\left(H\in BC\right)\). Chứng minh rằng :
a) HB = HC
b) \(\widehat{BAH}=\widehat{CAH}\)
a) Hai tam giác vuông ABH và ACH có:
AB=AC(gt)
AH cạnh chung.
Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)
Suy ra HB=HC
b)∆ABH=∆ACH(Câu a)
Suy ra ^BAH=^CAH(Hai góc tương ứng)
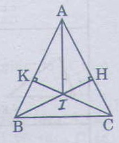
Cho tam giác ABC cân tại A \(\left(\widehat{A}< 90^0\right)\). Vẽ \(BH\perp AC\left(H\in AC\right),CK\perp AB\left(K\in AB\right)\)
a) Chứng minh rằng AH = AK
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là phân giác của góc A
a) Hai tam giác vuông ABH và ACK có:
AB = AC(gt)
Góc A chung.
nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)
suy ra AH = AK.
b) Hai tam giác vuông AIK và AIH có:
AK = AH(cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)
Suy ra ˆIAKIAK^=ˆIAHIAH^
Vậy AI là tia phân giác của góc A.
Trả lời bởi Nguyễn Trần Thành Đạt
Tam giác ABC có M là trung điểm của BC, AM là tia phân giác của góc A. Kẻ MH vuông góc với AB, MK vuông góc với AC. Chứng minh rằng :
a) \(MH=MK\)
b) \(\widehat{B}=\widehat{C}\)
a) Xết hai tam giác vuông AMH và AMK có:
AM: cạnh huyền chung
\(\widehat{HAM}=\widehat{KAM}\left(gt\right)\)
Vậy: \(\Delta AMH=\Delta AMK\left(ch-gn\right)\)
Suy ra: MH = MK (hai cạnh tương ứng)
b) Xét hai tam giác vuông MHB và MKC có:
MB = MC (gt)
MH = MK (cmt)
Vậy: \(\Delta MHB=\Delta MKC\left(ch-cgv\right)\)
Suy ra: \(\widehat{B}=\widehat{C}\) (hai góc tương ứng).
Trả lời bởi Hải Ngân
Xét hai tam giác vuông ABD và ACD có:
AD: cạnh chung
AB = AC (do \(\Delta ABC\) cân tại A)
Vậy: \(\Delta ABD=\Delta ACD\left(ch-cgv\right)\)
Suy ra: \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
Do đó AD là tia phân giác của góc A.
Trả lời bởi Hải Ngân