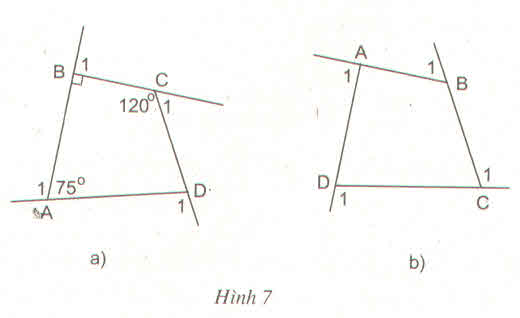
Ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{0}\)(Định lí tổng các góc trong tứ giác)
\(\Rightarrow\)\(\widehat{D}=360^{0}-(\widehat{A}+\widehat{B}+\widehat{C})\)
\(=360^{0}-(65^{0}+117^{0}+71^{0}) =107^{0}\)
Gọi \(\widehat{D_{1}}\) là góc ngoài tại đỉnh D của tứ giác ABCD. Ta có:
\(\widehat{D}+\widehat{D_{1}}=180^{0}\) (\(\widehat{D}\) và \(\widehat{D_{1}}\) là hai góc kề bù)
\(\Rightarrow\) \(\widehat{D_{1}}=180^{0}-\widehat{D}\)
\(=180^{0}-107^{0}=73^{0}\)
Vậy số đo góc ngoài tại đỉnh D của tứ giác ABCD là 730
Tứ giác ABCD có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(65^o+117^o+71^o+\widehat{D}=360^o\)
\(253^o+\widehat{D}=360^o\)
\(\widehat{D}=360^o-253^o=107^o\)
\(\Rightarrow\) Góc ngoài của \(\widehat{D}=180^o-107^o=73^o\)
Vậy số đo góc ngoài tại đỉnh D là \(73^o\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^O\) (định lí tứ giác)\
\(\Rightarrow\widehat{D}=360^o-65^o-117^o-71^o\)
\(\Rightarrow\widehat{D}=107^o\)
Gọi \(\widehat{D_1}\) là góc ngoài tại đỉnh D của tứ giác ABCD
\(\Rightarrow\widehat{D}+\widehat{D_1}=180^o\) (kề bù)
\(\Rightarrow\widehat{D_1}=180^o-107^o\)
\(\Rightarrow\widehat{D_1}=73^o\)
A+ˆB+ˆC+ˆD=3600A^+B^+C^+D^=3600(Định lí tổng các góc trong tứ giác)
⇒⇒ˆD=3600−(ˆA+ˆB+ˆC)D^=3600−(A^+B^+C^)
=3600−(650+1170+710)=1070=3600−(650+1170+710)=1070
Gọi ˆD1D1^ là góc ngoài tại đỉnh D của tứ giác ABCD. Ta có:
ˆD+ˆD1=1800D^+D1^=1800 (ˆDD^ và ˆD1D1^ là hai góc kề bù)
⇒⇒ ˆD1=1800−ˆDD1^=1800−D^
=1800−1070=730=1800−1070=730
Vậy số đo góc ngoài tại đỉnh D của tứ giác ABCD là 730