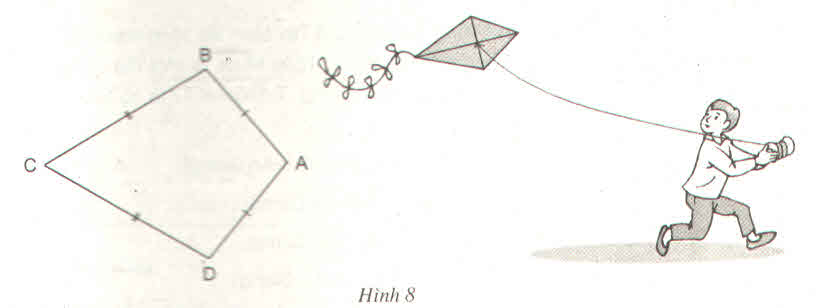
a) Ta có: \(AB=AD\left(gt\right)\)
=> \(A\) thuộc đường trung trực của \(BD\) (Theo tính chất một điểm cách đều hai đầu của đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó). (1)
\(CB=CD\left(gt\right)\)
=> \(C\) thuộc đường trung trực của \(BD\) (Theo tính chất một điểm cách đều hai đầu của đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó). (2)
Từ (1) và (2) => \(AC\) là đường trung trực của \(BD.\) b) Xét 2 \(\Delta\) \(ABC\) và \(ADC\) có: \(AB=AD\left(gt\right)\) \(BC=DC\left(gt\right)\) Cạnh AC chung => \(\Delta ABC=\Delta ADC\left(c-c-c\right)\) => \(\widehat{B}=\widehat{D}\) (2 góc tương ứng) Xét tứ giác \(ABCD\) có: \(\widehat{BAD}+\widehat{B}+\widehat{BCD}+\widehat{D}=360^0\) (định lí tổng các góc trong 1 tứ giác) => \(100^0+\widehat{B}+60^0+\widehat{D}=360^0\)=> \(\widehat{B}+\widehat{D}=360^0-\left(100^0+60^0\right)\) => \(\widehat{B}+\widehat{D}=360^0-160^0\) => \(\widehat{B}+\widehat{D}=200^0.\)
Mà \(\widehat{B}=\widehat{D}\left(cmt\right)\) => \(\widehat{B}+\widehat{B}=200^0\) => \(2.\widehat{B}=200^0\) => \(\widehat{B}=200^0:2\) => \(\widehat{B}=\widehat{D}=100^0.\) Vậy \(\widehat{B}=\widehat{D}=100^0.\) Chúc bạn học tốt!