a. Em tự giải
b.
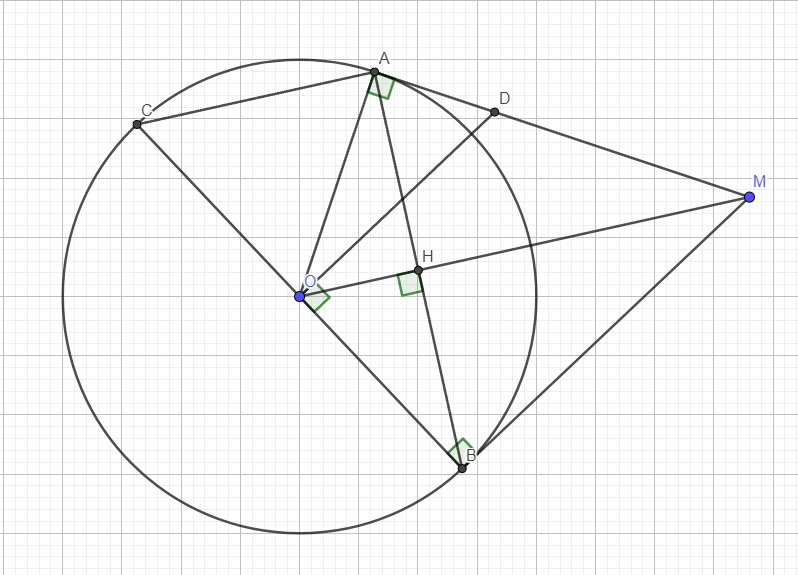
Do AMBO nội tiếp \(\Rightarrow\widehat{BOM}=\widehat{BAM}\) (cùng chắn AM)
Lại có \(\widehat{BAM}=\widehat{ACB}\) (cùng chắn AB của (O))
\(\Rightarrow\widehat{BOM}=\widehat{ACB}\)
c.
Gọi H là giao điểm OM và AB
Theo t/c hai tiếp tuyến cắt nhau: \(MA=MB\)
Đồng thời \(OA=OB=R\)
\(\Rightarrow OM\) là trung trực AB \(\Rightarrow OM\perp AB\) tại H
\(\Rightarrow\widehat{DOM}=\widehat{HBO}\) (cùng phụ \(\widehat{HOB}\))
Lại có \(\widehat{HBO}=\widehat{AMO}\) (cùng chắn AO của đường tròn ngoại tiếp AMBO)
\(\Rightarrow\widehat{DOM}=\widehat{AMO}\)
\(\Rightarrow\Delta DOM\) cân tại D
\(\Rightarrow DO=DM\)
d.
Giả sử tam giác MAB đều \(\Rightarrow\widehat{AMB}=60^0\)
\(\Rightarrow\widehat{AMO}=\dfrac{1}{2}\widehat{AMB}=30^0\)
Trong tam giác vuông AMO:
\(sin\widehat{AMO}=\dfrac{OA}{OM}\Rightarrow OM=\dfrac{OA}{sin\widehat{AMO}}=\dfrac{R}{sin30^0}=2R\)
Vậy để AMB đều thì M cách O 1 đoạn \(OM=2R\)
a: Xét tứ giác AOBM có \(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
nên OAMB là tứ giác nội tiếp
b: ta có: OAMB là tứ giác nội tiếp
=>\(\widehat{BOM}=\widehat{BAM}\)
Xét (O) có
\(\widehat{BAM}\) là góc tạo bởi tiếp tuyến AM và dây cung AB
\(\widehat{ACB}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{BAM}=\widehat{ACB}\)
=>\(\widehat{ACB}=\widehat{BOM}\)