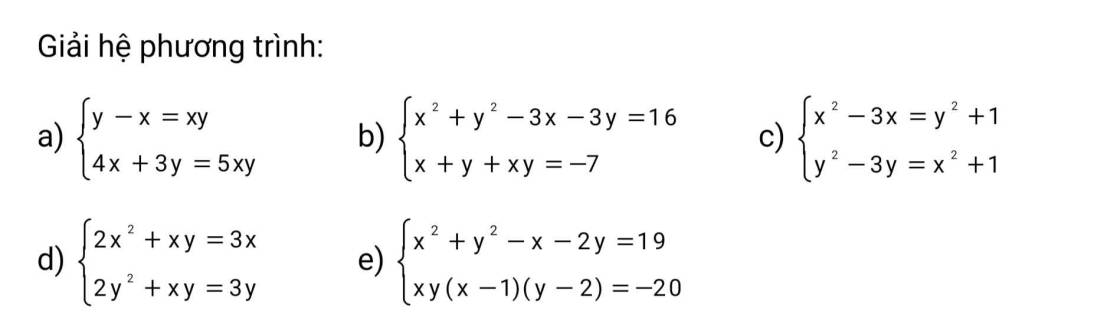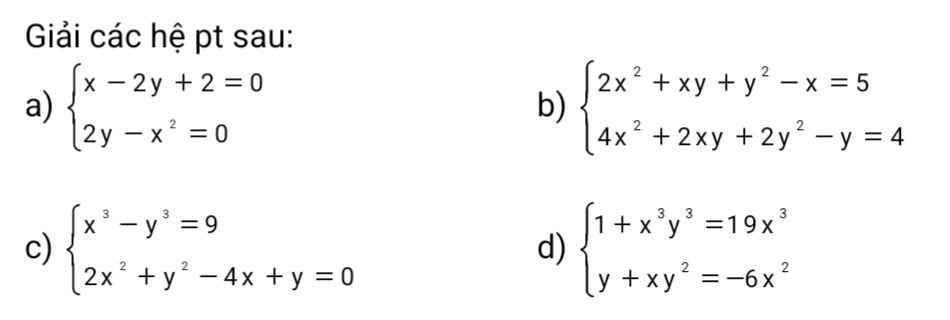a: Xét tứ giác AEDB có \(\widehat{AEB}=\widehat{ADB}=90^0\)
nên AEDB là tứ giác nội tiếp
=>A,E,D,B cùng thuộc một đường tròn
b: Ta có: AEDB là tứ giác nội tiếp
=>\(\widehat{ADE}=\widehat{ABE}\)
=>\(\widehat{HDE}=\widehat{ABN}\left(1\right)\)
Xét (O) có
\(\widehat{ABN}\) là góc nội tiếp chắn cung AN
\(\widehat{AMN}\) là góc nội tiếp chắn cung AN
Do đó: \(\widehat{ABN}=\widehat{AMN}=\widehat{HMN}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{HDE}=\widehat{HMN}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên DE//MN
c: Kẻ tiếp tuyến Cx của (O)
Xét (O) có
\(\widehat{xCB}\) là góc tạo bởi tiếp tuyến Cx và dây cung CB
\(\widehat{CAB}\) là góc nội tiếp chắn cung CB
Do đó: \(\widehat{xCB}=\widehat{CAB}\left(3\right)\)
Ta có: ABDE là tứ giác nội tiếp
=>\(\widehat{EDB}+\widehat{EAB}=180^0\)
mà \(\widehat{EDB}+\widehat{EDC}=180^0\)(hai góc kề bù)
nên \(\widehat{EDC}=\widehat{CAB}\left(4\right)\)
Từ (3) và (4) suy ra \(\widehat{EDC}=\widehat{xCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên DE//Cx
Ta có: OC\(\perp\)Cx
DE//Cx
Do đó: OC\(\perp\)DE
d: Xét (O) có
\(\widehat{AMB}\) là góc nội tiếp chắn cung AB
\(\widehat{ACB}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{AMB}=\widehat{ACB}\)
=>\(\widehat{BMH}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{AHE}\left(=90^0-\widehat{DAC}\right)\)
nên \(\widehat{BMH}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{BHM}\)(hai góc đối đỉnh)
nên \(\widehat{BMH}=\widehat{BHM}\)
=>ΔBMH cân tại B
Ta có: ΔBMH cân tại B
mà BC là đường cao
nên BC là đường trung trực của HM
=>H đối xứng M qua BC
Xét (O) có
\(\widehat{ANB}\) là góc nội tiếp chắn cung AB
\(\widehat{ACB}\)là góc nội tiếp chắn cung AB
Do đó: \(\widehat{ANB}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{BHD}\left(=90^0-\widehat{EBC}\right)\)
và \(\widehat{BHD}=\widehat{AHN}\)(hai góc đối đỉnh)
nên \(\widehat{AHN}=\widehat{ANH}\)
=>ΔANH cân tại A
Ta có: ΔANH cân tại A
mà AC là đường cao
nên AC la đường trung trực của NH
=>N đối xứng H qua AC
a) Ta có BE là đường cao của △BEA
⇒E ∈ đường tròn bán kính BA (1)
Ta có AD là đường cao của △ADB
⇒D ∈ đường tròn bán kính BA (2)
Từ (1) và (2) ta có: các điểm A,B,D,E cùng thuộc một đường tròn