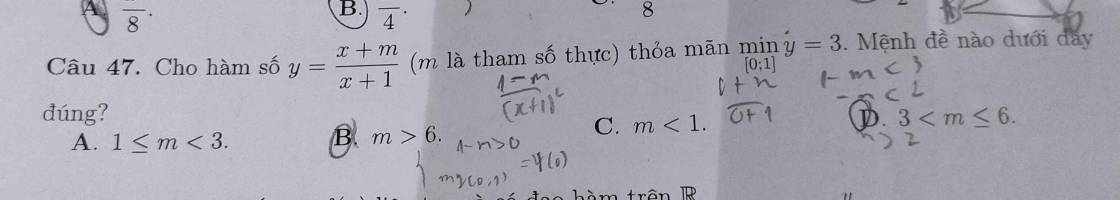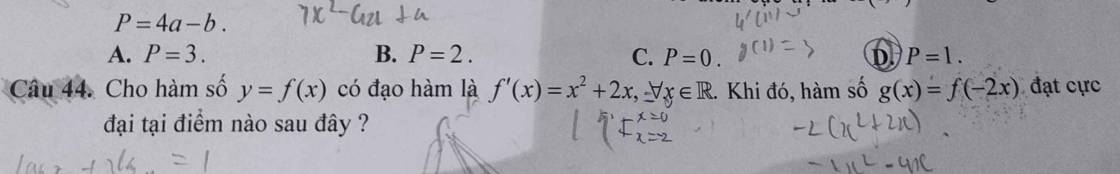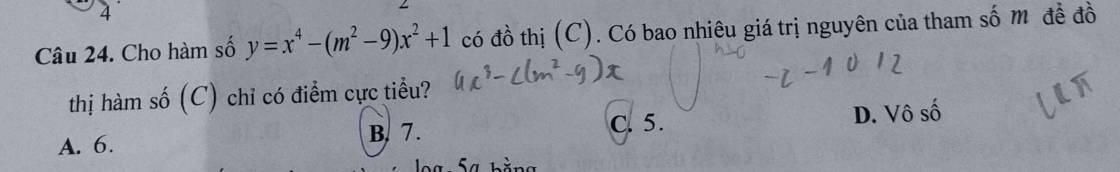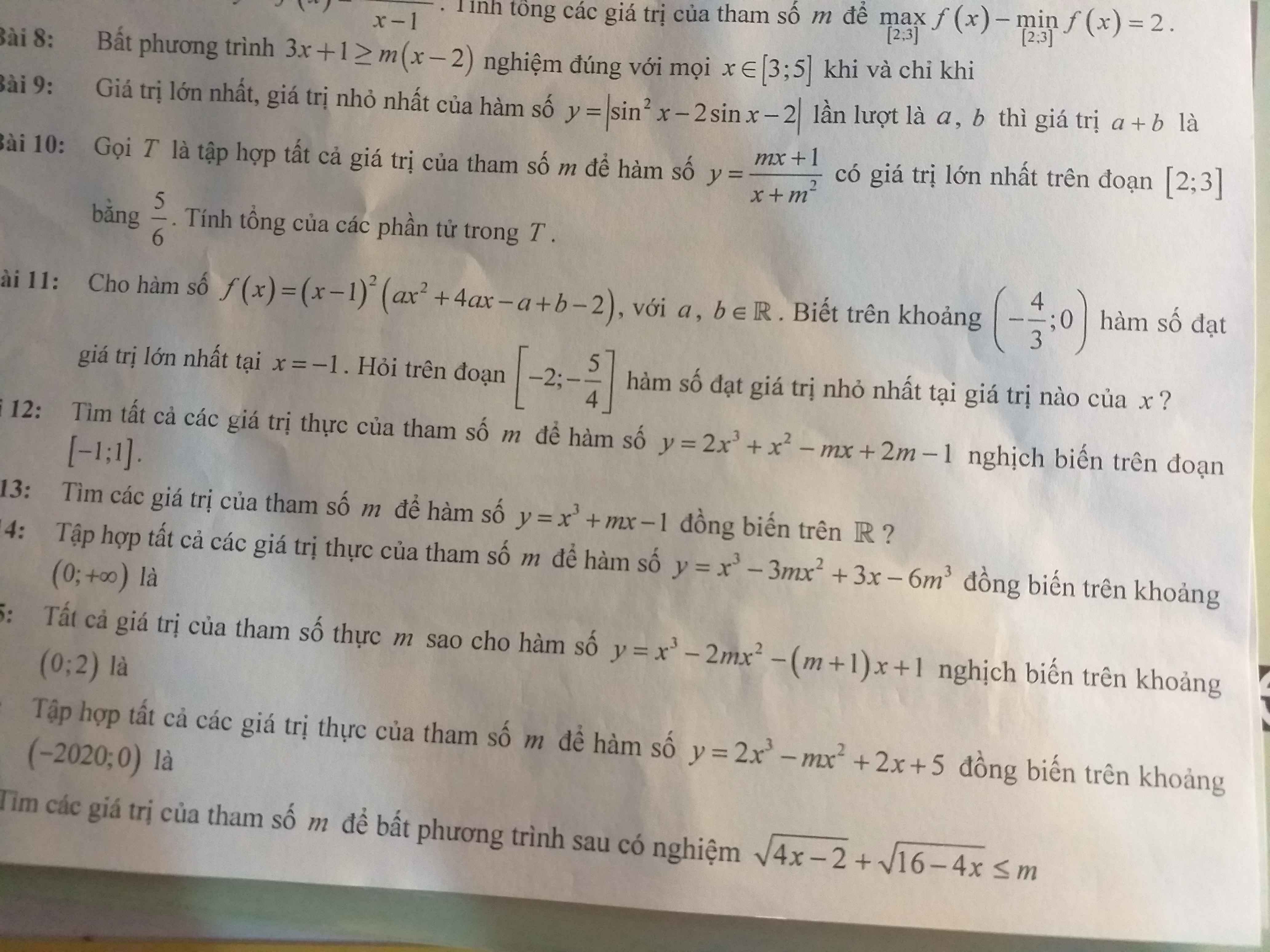54:
Gọi O là giao của AC và BD
ABCD là hình thoi
=>AC vuông góc BD tại O và O là trung điểm chung của AC và BD
\(\widehat{BAD}=180^0-120^0=60^0\)
Xét ΔABD có AB=AD và góc BAD=60 độ
nên ΔABD đều
=>\(AO=AB\cdot\dfrac{\sqrt{3}}{2}\)
=>\(AG=\dfrac{2}{3}\cdot AO=\dfrac{\sqrt{3}}{3}\cdot a\)
\(AA'=\sqrt{a^2-\left(\dfrac{a\sqrt{3}}{3}\right)^2}=\dfrac{a\sqrt{6}}{3}\)
\(S_{ABCD}=2\cdot S_{ABD}=AB\cdot AD\cdot sinBAD=\dfrac{a^2\sqrt{3}}{2}\)
\(V=\dfrac{a\sqrt{6}}{3}\cdot\dfrac{a^2\sqrt{3}}{2}=\dfrac{a^3\sqrt{2}}{2}\)
=>Chọn C
55:
ΔABC vuông tại B
=>\(S_{ABC}=\dfrac{1}{2}\cdot a\sqrt{3}\cdot a=\dfrac{a^2\sqrt{3}}{2}\)
\(V_{S.AHK}=\dfrac{1}{4}\cdot V_{ABC}=\dfrac{1}{4}\cdot\dfrac{1}{3}\cdot a\cdot\dfrac{a^2\sqrt{3}}{2}=\dfrac{a^3\sqrt{3}}{30}\)
=>B