giúp em với ạ!!!
`a) 3/5 :x -2/3 =4/4`
`3/5 :x = 4/4 +2/3 = 3/3 +2/3 =5/3`
`x = 3/5 :5/3 = 3/5 * 3/5 =9/25`
`b) 1/5 -1/2 (x-3)=1/3`
`1/2(x-3) = 1/5 -1/3 = -2/15`
`x-3 = -2/15 *2 = -4/15`
`x = -4/15 +3 = -4/15 + 45/15 = 41/15`
`c) (5^x)^2 = 25^11`
`5^(2x) = 5^22`
`2x=22`
`x=22/2=11`
`d) (x+1/5).|x-1| =0`
`=> [(x+1/5=0),(x-1=0):}`
`=> [(x=-1/5),(x=1):}`
Vậy `xin {-1/5;1}`
\(a,\dfrac{3}{5}:x-\dfrac{2}{3}=\dfrac{4}{4}< =>\dfrac{3}{5}:x=\dfrac{5}{3}< =>x=\dfrac{9}{25}\)
\(b,\dfrac{1}{5}-\dfrac{1}{2}.\left(x-3\right)=\dfrac{1}{3}< =>\dfrac{1}{2}.\left(x-3\right)=-\dfrac{2}{15}< =>x-3=-\dfrac{4}{15}< =>x=\dfrac{41}{15}\)
\(c,\left(5^x\right)^2=25^{11}< =>\left(5^x\right)^2=\left(5^2\right)^{11}< =>5^{x.2}=5^{2.11}< =>x.2=2.11< =>x.2=22< =>x=11\)
\(d,\left(x+\dfrac{1}{5}\right).\left|x-1\right|=0< =>\left[{}\begin{matrix}x+\dfrac{1}{5}=0\\x-1=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=-\dfrac{1}{5}\\x=1\end{matrix}\right.\)
`a) 3/5 : x - 2/3 = 4/4`
`=> 3/5 : x - 2/3 = 1`
`=> 3/5 : x = 1 + 2/3`
`=> 3/5 : x = 3/3 + 2/3`
`=> 3/5 : x = 5/3`
`=> x = 3/5 : 5/3`
`=> x = 3/5 xx 3/5`
`=> x = 9/25`
`b) 1/5 - 1/2 ( x - 3 ) = 1/3`
`=> 1/2 ( x - 3) = 1/5 - 1/3`
`=> 1/2 ( x - 3 ) = 3/15 - 5/15`
`=> 1/2 ( x - 3 ) = -2/15`
`=> x - 3 = -2/15 : 1/2`
`=> x - 3 = -2/15 xx 2`
`=> x - 3 = -4/15`
`=> x = -4/15 + 3`
`=> x = -4/15 + 45/15`
`=> x = 41/15`
`c) (5^x)^2 = 25^11`
`=> 5^(2x) = (5^2)^11`
`=> 5^(2x) = 5^22`
`=> 2x = 22`
`=> x = 22 :2 `
`=> x = 11`
`d) ( x + 1/5 ) . | x - 1 | = 0`
Trường hợp `1:`
`x+1/5=0`
`=>x=0-1/5`
`=>x=-1/5`
Trường hợp `2:`
`|x-1|=0`
`=>x-1=0`
`=>x=1`
Vậy `x in {-1/5;1}`
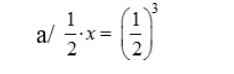giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
