\(\text{#TNam}\)
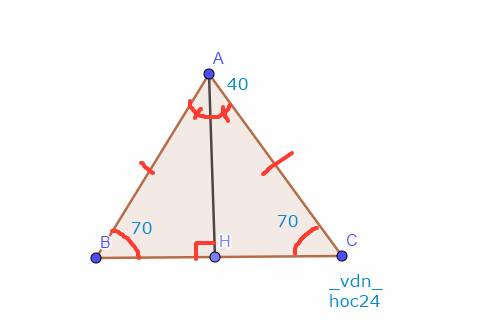
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC,`\(\widehat{B}=\widehat{C}\)
Mà \(\widehat{B}=70^0 \)`->`\(\widehat{C}=70^0\)
Xét Tam giác `ABC:`
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\widehat{A}+70^0+70^0=180^0\)
\(\widehat{A}=180^0-70^0-70^0\)
`->`\(\widehat{A}=40^0\)
`b,` cm Tam giác `AHB =` Tam giác `AHC` `?`
Xét Tam giác `AHB` và Tam giác `AHC` có:
`AB = AC (CMT)`
\(\widehat{B}=\widehat{C}=70^0\)
\(\widehat{BHA}=\widehat{CHA}=90^0\)
`=> \text {Tam giác AHB = Tam giác AHC (ch-gn)}`
`c,` \(\text{Vì Tam giác AHB = Tam giác AHC (b)}\)
`->`\(\widehat{BAH}=\widehat{CAH} (\text {2 góc tương ứng)}\)
`-> \text {AH là tia phân giác của}`\(\widehat{BAC}\)