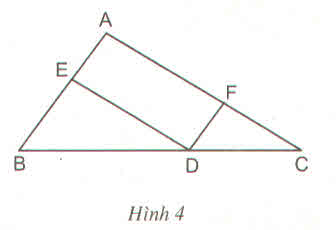
Trong ∆ ABC ta có: DE // AC (gt)
Suy ra: \(\frac{AE}{AB}=\frac{CD}{CB}\)(định lí Ta-lét) (1)
Lại có: DF // AB (gt)
Suy ra: \(\frac{AF}{AC}=\frac{BD}{BC}\)(định lí Ta-lét) (2)
Cộng trừ vế (1) và (2), ta có:
\(\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{BC}{BC}=1\)