Question

Cho tam giác ABC nội tiếp đường tròn. P, Q, R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.

a) Chứng minh \(AP\perp QR.\)

b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.

Answer 1

a) Gọi giao điểm của AP và QR là K.

\(\widehat{AKR}\) là góc có đỉnh ở bên trong đường tròn nên

\(\widehat{AKR}\) = sđcung(AR +QC + CP)/2 =

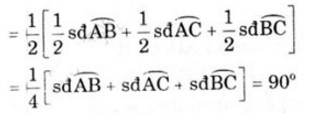
Vậy \(\widehat{AKR}\) = 900 hay AP \(\perp\) QR

b) \(\widehat{CIP}\) là góc có đỉnh ở bên trong đường tròn nên:

\(\widehat{CIP}\) = sđcung(AR +CP)/2 (1)

\(\widehat{PIC}\) góc nội tiếp, nên \(\widehat{PIC}\)= (sđ cung RB + BP)/2 (2)

Theo giả thiết thì cung AR = RB (3)

Cung CP = BP (4)

Từ (1), (2), (3), (4) suy ra: \(\widehat{CIP}\) = \(\widehat{PIC}\). Do đó \(\Delta\)CPI cân.