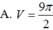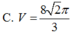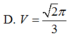Gọi O là tâm đáy, M là trung điểm AB
\(OA=\dfrac{a\sqrt{3}}{3}\) ; \(OM=\dfrac{1}{2}OA=\dfrac{a\sqrt{3}}{6}\)
\(\widehat{SMO}=45^0\Rightarrow SO=OM=\dfrac{a\sqrt{3}}{6}\)
\(SA=\sqrt{SO^2+OA^2}=\dfrac{a\sqrt{15}}{6}\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{5a\sqrt{3}}{12}\)
\(V=\dfrac{4}{3}\pi R^3=\dfrac{125\pi a^3\sqrt{3}}{432}\)