Bài giải:
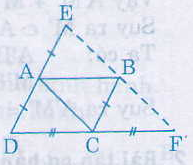
AE // BC (vì AD // BC)
AE = BC (cùng bằng AD)
nên ACBE là hình bình hành.
Suy ra: BE // AC, BE = AC (1)
Tương tự BF // AC, BF = AC (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF. Nên B là trung điểm của EF, vậy E đối xứng với F qua B.
AE//BC (vì AD//BC)
AE=BC (cùng bằng AD)
nên ACBE là hình bình hành theo dấu hiệu nhận biết hình bình hành.
Suy ra:BE//AC,BE=AC (1)
Tương tự BF//AC,BF=AC (2)
BE và BF cùng song song với AC và cùng đi qua điểm B nên theo tiên đề Ơ -clit BE trùng BF, hay B,E,F thẳng hàng.
Từ (1) và (2) BE=BFdo đó B là trung điểm của EF
Vậy E đối xứng với F qua B


AE//BCAE//BC (vì AD//BCAD//BC)
AE=BCAE=BC (cùng bằng ADAD)
nên ACBEACBE là hình bình hành theo dấu hiệu nhận biết hình bình hành.
Suy ra: BE//AC,BE=ACBE//AC,BE=AC (1)
Tương tự BF//AC,BF=ACBF//AC,BF=AC (2)
BEBE và BFBF cùng song song với ACAC và cùng đi qua điểm BB nên theo tiên đề Ơ -clit BEBEtrùng BFBF, hay B,E,FB,E,F thẳng hàng.
Từ (1) và (2) BE=BFBE=BF do đó BB là trung điểm của EFEF.
Vậy EE đối xứng với FF qua BB.



