Bài giải:
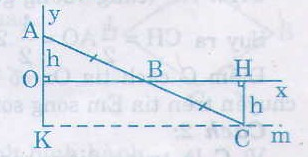
Kẻ AH và CK vuông góc với d.
Ta có AB = CB (gt)
ˆABHABH^ = ˆCBKCBK^ ( đối đỉnh)
nên ∆AHB = ∆CKB (cạnh huyền - góc nhọn)
Suy ra CK = AH = 2cm
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.
68. Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. lấy điểm B bất kì thuộc đường thằng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào ?
Bài giải:

Kẻ AH và CK vuông góc với d.
Ta có AB = CB (gt)
ˆABHABH^ = ˆCBKCBK^ ( đối đỉnh)
nên ∆AHB = ∆CKB (cạnh huyền - góc nhọn)
Suy ra CK = AH = 2cm
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.
Giải :
Kẻ AH\(\perp\)d,CK\(\perp\)d
Vì AH\(\perp\) d \(\Rightarrow\Delta AHB\) vuông tại H
CK\(\perp d\Rightarrow\Delta BKC\) vuông tại K
Xét \(\Delta AHB\)vuông tại H và\(\Delta BKC\)vuông tại K có:
AB=CD (C đối xứng A qua B)
góc ABH= góc CBK (đối đỉnh)
=>\(\Delta AHB=\)\(\Delta BKC\) (ch-gn)
=>CK=AH
Mà AH=2cm
=>CK=AH=2cm
Điểm C cách đường thẳng d cố định 1 khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng M song song với d và cách đường thẳng d một khoảng bằng 2cm.
Kẻ AH và CK vuông góc với dd.
Vì C là điểm đối xứng với A qua B (gt)
⇒AB=CB (tính chất hai điểm đối xứng qua 1 điểm)
Xét hai tam giác vuông AHB và CKB có:
AB=CB (cmt)
\(\widehat{ABH}=\widehat{CBK}\) ( đối đỉnh)
nên ∆AHB=∆CKB (cạnh huyền - góc nhọn)
⇒ CK=AH=2cm (2 cạnh tương ứng)
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.

