Ôn tập góc với đường tròn
Các câu hỏi tương tự
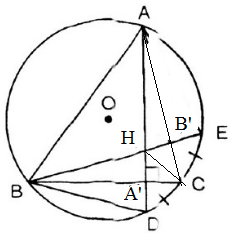
Cho ∆ ABC có 3 góc nhọn nội tiếp (O) các đường cao kẽ từ A và B của A cắt nhau tại H và cắt (O) lần lượt tại D và E. Chứng minh :
a) CD = CE
b) ∆ BHD cân
c) CD=CH
Cho ∆ ABC có 3 góc nhọn nội tiếp (O) các đường cao kẽ từ A và B của A cắt nhau tại H và cắt (O) lần lượt tại D và E. Chứng minh:
a) CD = CE
b) ∆ BHD cân
c) CD = CH
Cho tam giác ABC nội tiếp đường tròn (O) . Hai đường cao BD,CE cắt nhau tại H Và cắt đường tròn lần lượt ở M và N.
Cm: a, Tam giác AMN cân.
b, H và M đối xứng M qua AC và H đối xứng N qua AB.
c, OA vuông góc với DE
![]()
Các đường cao AN và BM của tam giác ABC có ba góc nhọn cắt nhau tại H và và cắt (O;R) ngoại tiếp tam giác ABC lần lượt tại D và E. a) Chứng minh CD = CE. b) Chứng minh H và D đối xứng nhau qua BC c) Chứng minh MN song song với DE d) Biết MN/AB = 1/2. Tính MN theo R
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Hai đường cao AD và BE cắt nhau tại H. Ad cắt đường tròn tại F. Chứng minh: a) Tứ giác ABDE nội tiếp được trong một đường tròn b) DA.DF=DB.DC c) ∆BHF cân
Cho đường tròn tâm O .Kẻ đường kính AB và CD vuông góc với nhau . Gọi E là điểm chính giữa cung nhỏ CD .EA cắt CD tại F ;ED cắt AB tại M
a/ Các tam giác CEF và EMB là những tam giác gì ?
b/ chứng minh bốn điểm D , C, M ,B thuộc đường tròn tâm E .
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm . Hai đường cao AM và CF của tam giác ABC cắt nhau tại H và cắt (O) lần lượt tại Q và D. Chứng minh:
a. BFHM nội tiếp
b. ACMF nội tiếp
c. BC là tia phân giác của HBQ
cho tam giác abc nhọn ab lớn hơn ac nội tiếp đường tròn đường kính ad đường cao cf và bg cắt nhau tại h kẻ oi vuông góc bc a) chứng minh tứ giác cgfb nội tiếp đường tròn b)chứng minh tam giác acd đồng dạng tam giác cfb c)chứng minh tứ giác chbd là hình bình hành và cd.cg=bd.bf d) chứng minh i,h,d thẳng hàng
cho tam giác ABC nhọn AB<AC nội tiếp đường tròn tâm O. BD và CE là đường cao cắt nhau tại H . K là giao điểm của CB và ED .
a) B,E,C,D thuộc đường tròn tâm M
b) cm KB.KC=KE.KD