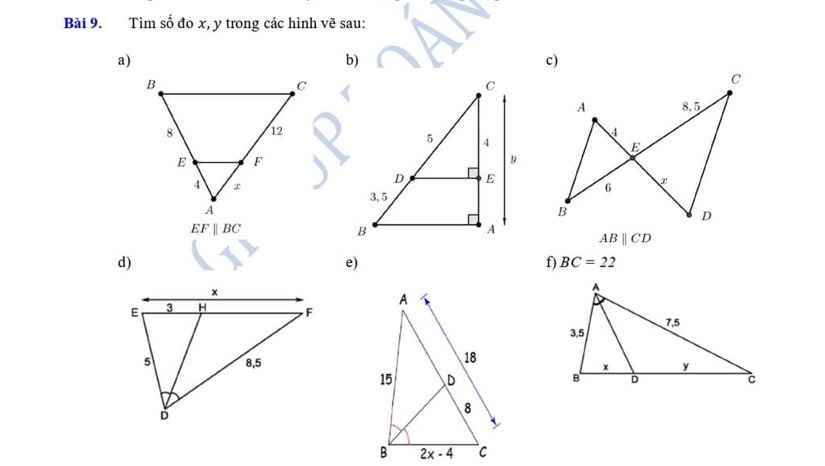
a: Xét ΔABC có EF//BC
nên \(\dfrac{AF}{FC}=\dfrac{AE}{EB}\)
=>\(\dfrac{x}{12}=\dfrac{4}{8}=\dfrac{1}{2}\)
=>x=12/2=2=6
b: CB=CD+DB
=5+3,5
=8,5
Xét ΔCAB có DE//AB
nên \(\dfrac{CE}{CA}=\dfrac{CD}{CB}\)
=>\(\dfrac{4}{y}=\dfrac{5}{8,5}\)
=>\(y=\dfrac{4\cdot8,5}{5}=\dfrac{34}{5}=6,8\)
c: Xét ΔEAB và ΔEDC có
\(\widehat{EAB}=\widehat{EDC}\)(hai góc so le trong, AB//DC)
\(\widehat{AEB}=\widehat{DEC}\)(hai góc đối đỉnh)
Do đó: ΔEAB đồng dạng với ΔEDC
=>\(\dfrac{EA}{ED}=\dfrac{EB}{EC}\)
=>\(\dfrac{4}{x}=\dfrac{6}{8,5}\)
=>\(x=4\cdot\dfrac{8.5}{6}=\dfrac{17}{3}\)
d: Xét ΔDEF có DH là phân giác
nên \(\dfrac{HE}{ED}=\dfrac{HF}{FD}\)
=>\(\dfrac{HF}{8,5}=\dfrac{3}{5}\)
=>HF=8,5*3/5=5,1
x=EF=EH+HF=3+5,1=8,1
e:
DC+DA=AC
=>DA+8=18
=>DA=10
Xét ΔBCA có BD là phân giác
nên \(\dfrac{BC}{CD}=\dfrac{BA}{AD}\)
=>\(\dfrac{BC}{BA}=\dfrac{CD}{AD}\)
=>\(\dfrac{BC+BA}{BA}=\dfrac{CD+AD}{AD}\)
=>\(\dfrac{2x-4+15}{15}=\dfrac{18}{10}=\dfrac{9}{5}\)
=>\(2x+11=\dfrac{9}{5}\cdot15=9\cdot3=27\)
=>2x=16
=>x=8
f: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{x}{3,5}=\dfrac{y}{7,5}\)
mà x+y=BC=22
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3,5}=\dfrac{y}{7,5}=\dfrac{x+y}{3,5+7,5}=\dfrac{22}{11}=2\)
=>\(x=2\cdot3,5=7;y=2\cdot7,5=15\)