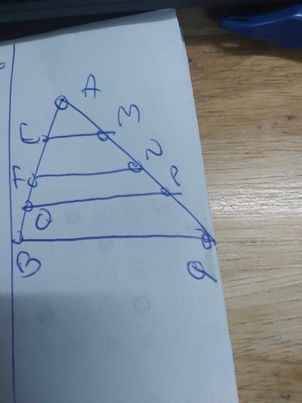
a: Kẻ ME//BQ(E\(\in\)AB), NF//BQ(F\(\in\)AB),PO//BQ(O\(\in AB\))
Khi kẻ hình như vậy thì ta sẽ được AE=EF=FO=OB=AB/4
=>Ta sẽ được 4 đoạn bằng nhau cần chia
b: Giải thích:
Theo hình vẽ ban đầu, ta sẽ có được:
\(AM=MN=NP=PQ=\dfrac{AQ}{4}\)
AM=MN nên M là trung điểm của AN
=>\(AM=\dfrac{1}{2}AN\)
NP=PQ
=>P là trung điểm của NQ
Xét ΔABC có EM//BQ
nên \(\dfrac{AE}{AB}=\dfrac{AM}{AQ}=\dfrac{1}{4}\)
=>\(AE=\dfrac{1}{4}AB\)
Xét ΔABQ có NF//BQ
nên \(\dfrac{AF}{AB}=\dfrac{AN}{AQ}\)
=>\(\dfrac{AF}{AB}=\dfrac{1}{2}\)
=>\(AF=\dfrac{1}{2}AB\)
mà \(AE=\dfrac{1}{4}AB\)
nên \(\dfrac{AF}{AE}=\dfrac{1}{2}:\dfrac{1}{4}=2\)
=>AF=2AE
=>E là trung điểm của AF
=>EF=AE=1/4AB
AF+FB=AB
=>\(FB+\dfrac{1}{2}AB=AB\)
=>\(FB=\dfrac{1}{2}AB\)
Xét hình thang FNQB có
P là trung điểm của NQ
PO//FN//BQ
Do đó: O là trung điểm của FB
=>\(OF=OB=\dfrac{BF}{2}=\dfrac{1}{4}AB\)
=>\(AE=EF=FO=OB=\dfrac{1}{4}AB\)(ĐPCM)



