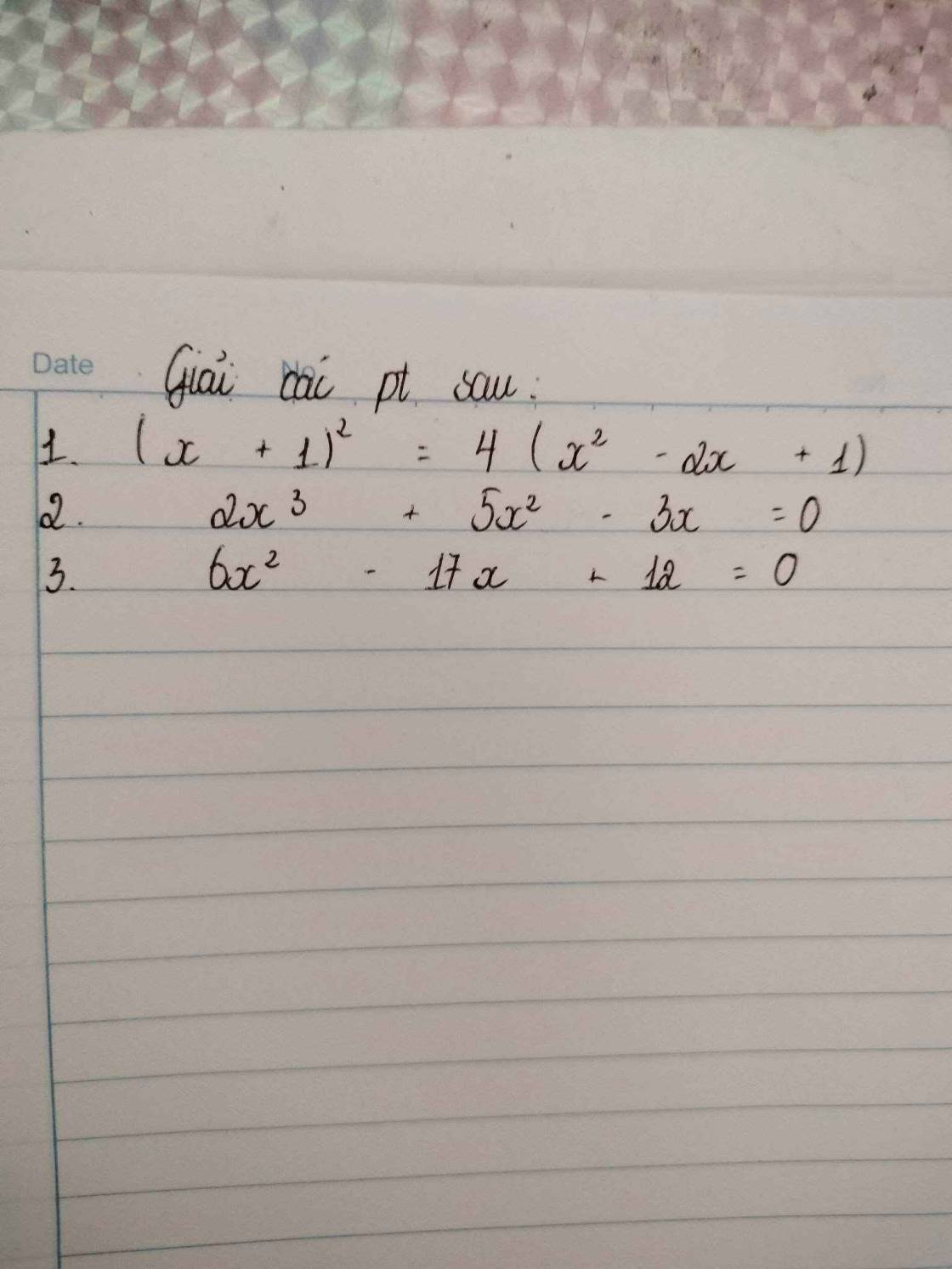Giải :
\(1,\left(x+1\right)^2=4\left(x^2-2x+1\right)\\ \Leftrightarrow x^2+2x+1=4x^2-8x+4\\ \Leftrightarrow-3x^2+10x-3=0\\ \Leftrightarrow-3x^2+9x+x-3=0\\ \Leftrightarrow-3x\left(x-3\right)+\left(x-3\right)=0\\ \Leftrightarrow\left(1-3x\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}1-3x=0\\x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=3\end{matrix}\right.\)
\(2,2x^3+5x^2-3x=0\\ \Leftrightarrow2x^3+6x^2-x^2-3x=0\\ \Leftrightarrow2x^2\left(x+3\right)-x\left(x+3\right)=0\\ \Leftrightarrow\left(2x^2-x\right)\left(x+3\right)=0\\ \Leftrightarrow x\left(2x-1\right)\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\2x-1=0\\x+3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=-3\end{matrix}\right.\)
\(3,6x^2-17x+12=0\\ \Leftrightarrow6x^2-8x-9x+12=0\\ \Leftrightarrow2x\left(3x-4\right)-3\left(3x-4\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(3x-4\right)=0\\\Leftrightarrow \left[{}\begin{matrix}2x-3=0\\3x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{4}{3}\end{matrix}\right.\)
1)
`(x+1)^2 =4(x^2 -2x+1)`
<=> x^2 +2x+1=4x^2 -8x+4`
`<=> 4x^2 -x^2 -8x -2x +4 -1 =0`
`<=> 3x^2 -10x +3=0`
`<=> 3x^2 -9x-x+3=0`
`<=> 3x(x-3)-(x-3)=0`
`<=> (x-3)(3x-1)=0`
\(< =>\left[{}\begin{matrix}x-3=0\\3x-1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=3\\x=\dfrac{1}{3}\end{matrix}\right.\)
2)
`2x^3 +5x^2 -3x=0`
`<=> x(2x^2 +5x-3)=0`
`<=> x(2x^2 +6x-x-3)=0`
`<=> x[2x(x+3)-(x+3)]=0`
`<=> x(x+3)(2x-1)=0`
\(< =>\left[{}\begin{matrix}x=0\\x+3=0\\2x-1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=-3\\x=\dfrac{1}{2}\end{matrix}\right.\)
3)
`6x^2 -17x+12=0`
`<=> 6x^2 -9x-8x+12=0`
`<=> 3x(2x-3)-4(2x-3)=0`
`<=> (2x-3)(3x-4)=0`
\(< =>\left[{}\begin{matrix}2x-3=0\\3x-4=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{4}{3}\end{matrix}\right.\)
\(1)\left(x+1\right)^2=4\left(x^2-2x+1\right)\)
\(\Leftrightarrow x^2+2x+1=4x^2-8x+4\)
\(\Leftrightarrow x^2+2x+1-4x^2+8x-4=0\)
\(\Leftrightarrow10x-3x^2-3=0\)
\(\Leftrightarrow-3x^2+10x-3=0\)
\(\Leftrightarrow-3x^2+9x+x-3=0\)
\(\Leftrightarrow\left(-3x^2+9x\right)+\left(x-3\right)=0\)
\(\Leftrightarrow3x\left(x-3\right)+\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\3x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{-1}{3}\end{matrix}\right.\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{3;\dfrac{-1}{3}\right\}\)
\(2)2x^3+5x^2-3x=0\)
\(\Leftrightarrow2x^3+6x^2-x^2-3x=0\)
\(\Leftrightarrow\left(2x^3+6x^2\right)-\left(x^2+3x\right)=0\)
\(\Leftrightarrow2x^2\left(x+3\right)-x\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(2x^2-x\right)=0\)
\(\Leftrightarrow\left(x+3\right)x\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=0\\2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{-3;0;\dfrac{1}{2}\right\}\)
\(3)6x^2-17x+12=0\)
\(\Leftrightarrow6x^2-8x-9x+12=0\)
\(\Leftrightarrow\left(6x^2-8x\right)-\left(9x-12\right)=0\)
\(\Leftrightarrow2x\left(3x-4\right)-3\left(3x-4\right)=0\)
\(\Leftrightarrow\left(3x-4\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-4=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=4\\2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=\dfrac{3}{2}\end{matrix}\right.\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{\dfrac{4}{3};\dfrac{3}{2}\right\}\)