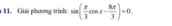Lời giải:
$y=2\sin ^2x+\cos x-3$
$=2(1-\cos ^2x)+\cos x-3$
$=-2\cos ^2x+\cos x-1$
Đặt $\cos x=a$ với $a\in [-1;1]$ thì cần tìm min, max của:
$y=-2a^2+a-1$
Ta thấy:
$y=\frac{-7}{8}-2(a-\frac{1}{4})^2\leq \frac{-7}{8}$ với mọi $a\in [-1;1]$ nên $y_{\max}=\frac{-7}{8}$
$y=(3-2a)(a+1)-4\geq -4$ với mọi $-1\leq a\leq 1$
Do đó $y_{\min}=-4$