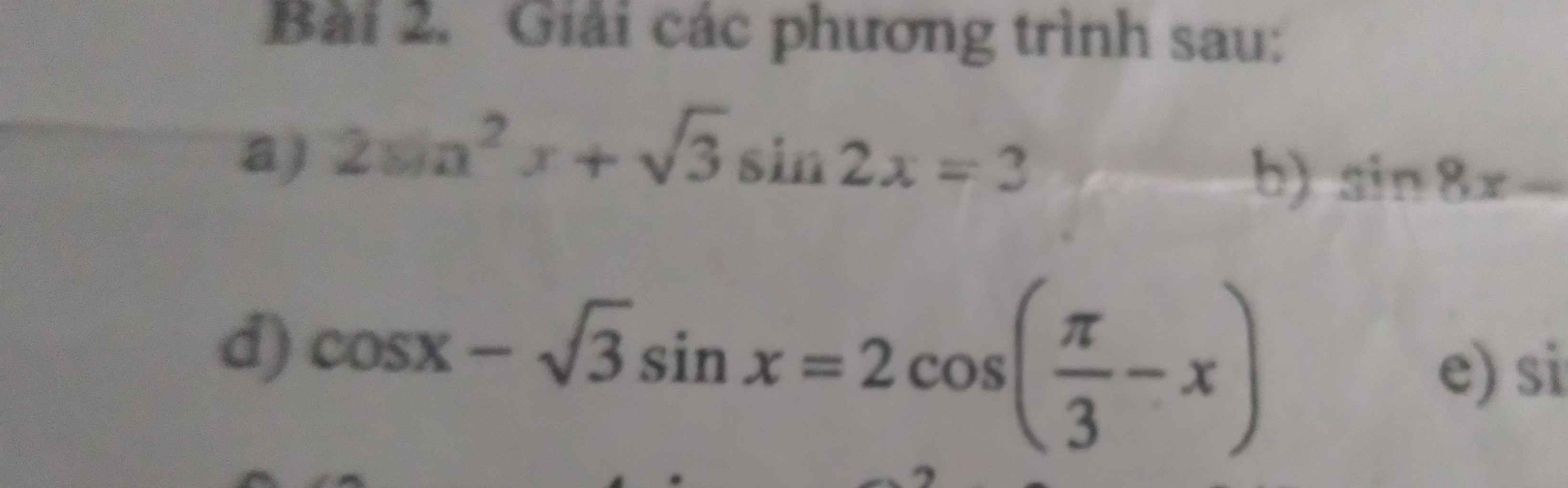`(1+2cosx)(3-cosx)=0`
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\cosx=3\left(L\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2\pi}{3}+k2\pi\\x=\dfrac{-2\pi}{3}+k2\pi\end{matrix}\right.\\ \Leftrightarrow x=\dfrac{2\pi}{3}+k\pi\)
`(k \in ZZ)`
\(\Leftrightarrow\left[{}\begin{matrix}1+2\cos x=0\\3-\cos x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos x=-\dfrac{1}{2}\\\cos x=3\end{matrix}\right.\)
Mà \(-1\le\cos x\le1\)
\(\Rightarrow\cos x=-\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\pi+k2\pi\\x=\dfrac{4}{3}\pi+k2\pi\end{matrix}\right.\)
Vậy ...