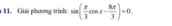1.
a, \(2sin\left(3x-\dfrac{\pi}{6}\right)=\sqrt{3}\)
\(\Leftrightarrow sin\left(3x-\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\3x-\dfrac{\pi}{6}=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\\x=\dfrac{5\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
1.
c, ĐK: \(x\ne\dfrac{k\pi}{2};x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
\(tan3x=cot2x\)
\(\Leftrightarrow tan3x=tan\left(\dfrac{\pi}{2}-2x\right)\)
\(\Leftrightarrow3x=\dfrac{\pi}{2}-2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{10}+\dfrac{k\pi}{5}\)
1.
e, \(cosx.cos2x.cos4x.cos8x=\dfrac{1}{16}\)
\(\Leftrightarrow16cosx.cos2x.cos4x.cos8x=1\)
Nếu \(sinx=0\Rightarrow\) phương trình vô nghiệm.
Nếu \(sinx\ne0\), phương trình tương đương:
\(\Leftrightarrow16sinx.cosx.cos2x.cos4x.cos8x=sinx\)
\(\Leftrightarrow8sin2x .cos2x.cos4x.cos8x=sinx\)
\(\Leftrightarrow4sin4x.cos4x.cos8x=sinx\)
\(\Leftrightarrow2sin8x.cos8x=sinx\)
\(\Leftrightarrow sin16x=sinx\)
\(\Leftrightarrow\left[{}\begin{matrix}16x=x+k2\pi\\16x=\pi-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k2\pi}{15}\\x=\dfrac{\pi}{17}+\dfrac{k2\pi}{17}\end{matrix}\right.\)
1.
g, \(sinx+cosx=\sqrt{2}sin4x\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}sin4x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=sin4x\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=x+\dfrac{\pi}{4}+k2\pi\\4x=\pi-x-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+\dfrac{k2\pi}{3}\\x=\dfrac{3\pi}{20}+\dfrac{k2\pi}{5}\end{matrix}\right.\)