Bài 9: Tính chất ba đường cao của tam giác

Trong ΔABC ta có ∠AC > ∠AB (gt)

Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)

Trong ΔAHB có ∠(AHB) = 90o

Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)

Trong ΔAHC có ∠(AHC) = 90o

Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)

Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .

Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.

Suy ra: AD ⊥ BC

Ta có: CH ⊥ AB (gt)

Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC

Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.

Vậy BD ⊥ AC.

Giải

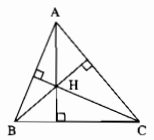
Trong ∆ABC ta có H là trực tâm nên

\(\text{ AH⊥BC,BH⊥AC,CH⊥AB}\)

Trong ∆AHB ta có:

Hai đường cao kẻ từ A và B cắt nhau tại C.

Vậy C là trực tâm của ∆AHB.

Trong ∆HAC ta có:

Hai đường cao kẻ từ A và C cắt nhau tại B, Vậy B là trực tâm của ∆HAC.

Trong ∆HBC ta có:

Hai đường cao kẻ từ B và C cắt nhau tại A. Vậy A là trực tâm của ∆HBC.

D

Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E

a) ∆HBC có:

HN ⊥ BC nên HN là đường cao

BE ⊥ HC nên BE là đường cao

CM ⊥ BH nên CM là đường cao

Vậy A là trực tâm của ∆HBC

b) Tương tự trực tâm của ∆AHB là C, ∆AHC là B

Trực tâm của ΔABC là đỉnh A

Trực tâm của ΔAHB là đỉnh H

Trực tâm của ΔAHC là đỉnh H

Trực tâm của tam giác vuông trùng với đỉnh góc vuông là vì mỗi cạnh góc vuông của tam giác chính là đường cao cua tam giác nên 2 cạnh góc vuông và đường cao ứng với cạnh huyền trong tam giác vuông cắt nhau tại đỉnh góc vuông.

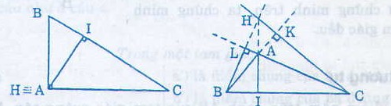
+ Nếu tam giác ABC có góc A tù => BC là cạnh lớn nhất

=> BC > BA

Kẻ đường cao BL thì LA; LC là hai hình chiếu của BA, BC => LA < LC

=> A nằm giữa L và C tức đường cao BL nằm ngoài tam giác ABC

Tương tự đường cao CK nằm ngoài tam giác ABC

Nên điểm cắt nhau của ba đường cao nằm ngoài tam giác

Giải tương tự như bài tập 59

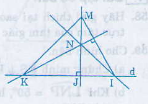
∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK

a) △ABC có : Hai đường cao BE và AD mà 2 đường này cùng cắt nhau tại điểm I ⇒ I là trực tâm

⇒ CI là đường cao còn lại ⇒ CI ⊥ AB

b) Xét △BEC có : góc EBC + gócBEC + góc BCE = \(180^0\)( định lí tổng ba góc )

⇒ góc EBC = \(180^0\) - góc BEC - góc BCE = \(180^0\)- \(90^0\)-\(40^0\)= \(50^0\)

Lại xét △BID có : góc BID + góc IBD + góc BDI = \(180^0\)

⇒ góc BID = \(180^0\) - \(90^0\) - \(50^0\) = \(40^0\)

Có góc BID + góc DIE = \(180^0\)( 2 góc kề bù )

⇒ góc DIE = \(180^0\) - góc BID = \(180^0-40^0\)= \(140^0\)

Tam giác ABC có AC=AB=13cm nên tam giác ABC cân tại A

=>đường trung tuyến của AM cũng là đường cao

=>AM \(\perp BC\)

Ta có MB=MC=1/2BC=1/2.10=5(cm)

Trong tam giác vuông AMB có góc vuông AMB=\(90^0\)

Áp dụng định lý Pitago ta có:

\(AB^2=AM^2+MB^2\)

=>\(AM^2=ÂB^2-MB^2\)

=\(13^2-5^2=169-25=144\)

Vậy AM=12 (cm)