Giải
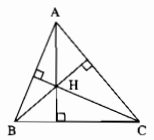
Trong ∆ABC ta có H là trực tâm nên
\(\text{ AH⊥BC,BH⊥AC,CH⊥AB}\)
Trong ∆AHB ta có:
\(\text{AC⊥BH }\)
\(\text{BC⊥AH}\)
Hai đường cao kẻ từ A và B cắt nhau tại C.
Vậy C là trực tâm của ∆AHB.
Trong ∆HAC ta có:
\(\text{BA⊥CH}\)
\(\text{CB⊥BH}\)
Hai đường cao kẻ từ A và C cắt nhau tại B, Vậy B là trực tâm của ∆HAC.
Trong ∆HBC ta có:
\(\text{BA⊥HC}\)
\(\text{CA⊥BH}\)
Hai đường cao kẻ từ B và C cắt nhau tại A. Vậy A là trực tâm của ∆HBC.
Đúng 0
Bình luận (0)