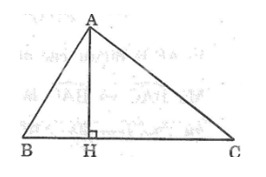
Trong ΔABC ta có ∠AC > ∠AB (gt)
Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ΔAHB có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong ΔAHC có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .