Cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE
a) Chứng minh rằng BE = CD
b) Gọi O là giao điểm của BE và CD. Chứng minh rằng \(\Delta BOD=\Delta COE\)
Cho hình 56.
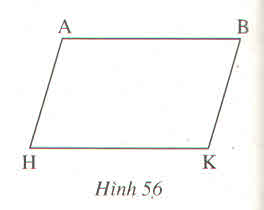
Trong đó AB // HK, AH // BK. Chứng minh rằng AB = HK, AH = BK ?
Nối A với K
Xét tam giác ABK và tam giác AHK có:
AK: cạnh chung
góc BAK = góc AKH (AB // HK)
góc HAK = góc AKB (AH //BK)
=> tam giác ABK = tam giác AHK
=> AB = HK (hai cạnh tương ứng)
Ta có: tam giác ABK = tam giác AHK
=> AH = BK (hai cạnh tương ứng)
Trả lời bởi Trương Hồng HạnhCho tam giác ABC ( \(\left(AB\ne AC\right)\), tia Ax đi qau trung điểm M của BC. Kẻ BE và CF vuông góc với Ax \(\left(E\in Ax,F\in Ax\right)\). So sánh các độ dài của BE và CF ?
Hai tam giác vuông BME, CMF có:
BM=MC(gt)
ˆBMEBME^=ˆCMFCMF^(đối đỉnh)
Nên ∆BME=∆CMF(cạnh huyền- góc nhọn).
Suy ra BE=CF.
Cho hình 57, chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC
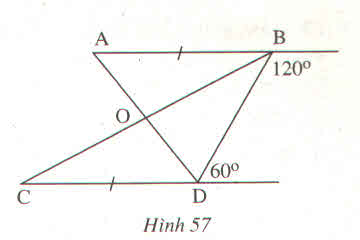
Ta có: góc B + góc D = 1200 + 600 = 1800
Mà hai góc này TCP
=> AB // CD
Xét tam giác ABO và tam giác CDO có:
AB = CD (GT)
ABC = BCD (AB // CD)
BAD = ADC (AB // CD)
=> tam giác ABO = tam giác CDO
=> AO = OD
=> O là trung điểm AD
Ta có: tam giác ABO = tam giác CDO
=> BO = OC
=> O là trung điểm BC
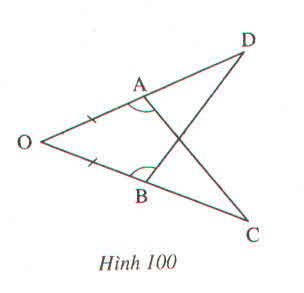
Trả lời bởi Trương Hồng HạnhTrên hình 100 ta có \(OA=OB;\widehat{OAC}=\widehat{OBD}\)
Chứng minh rằng AC = BD ?
Cho tam giác ABC có \(\widehat{A}=90^0\) (h.109). Kẻ AH vuông góc với BC (\(H\in BC\) ). Các tam giác AHC và BAC có AC là cạnh chung. \(\widehat{C}\) là góc chung, \(\widehat{AHC}=\widehat{BAC}=90^0\), nhưng hai tam giác đó không bằng nhau
Tại sao ở đây không thể áp dụng trường hợp góc - cạnh - góc để kết luận \(\Delta AHC=\Delta BAC\) ?
Vẽ tam giác ABC biết \(AC=2cm,\widehat{A}=90^0,\widehat{C}=60^0\) ?
Cách vẽ: 
– Vẽ đoạn AC=2cm,
– Trên cùng một nửa mặt phẳng bờ AC vẽ tia Ax và Cy sao cho góc ∠CAx = 900, ∠ACy = 600
Hai tia cắt nhau ở B. tạo thành tam giác ABC cần vẽ.
Trả lời bởi Quang DuyCho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot, nó cắt Ox và Oy theo thứ tự ở A và B
a) Chứng minh rằng OA = OB
b) Lấy điểm C thuộc tia Ot, chứng minh rằng CA = CB và \(\widehat{OAC}=\widehat{OBC}\)
a) ∆AOH và ∆BOH có:
∠AOH = ∠BOH (gt)
OH là cạnh chung
∠AHO = ∠OHB (=900)
∆AOH =∆BOH( g.c.g)
Vậy OA=OB.
b) ∆AOC và ∆BOC có:
OA = OB(cmt)
∠AOC = ∠BOC(gt)
OC cạnh chung.
Nên ∆AOC= ∆BOC(c.g.c)
Suy ra: CA=CB(cạnh tương ứng)
∠OAC = ∠OAB( góc tương ứng).
Trả lời bởi Quang DuyTrên mỗi hình 105, 106, 107, 108 có các tam giác vuông nào bằng nhau ? Vì sao ?
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở O. Kẻ \(OD\perp AC;OE\perp AB\).
Chứng minh rằng OD = OE ?
Giải
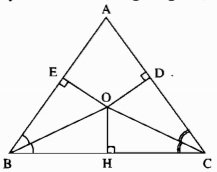
Kẻ OH⊥BC
Xét hai tam giác vuông OEB và OHB, ta có:
\(\widehat{\text{OEB}}=\widehat{\text{OHB}}\)=90o
Cạnh huyền OB chung
\(\widehat{EBO}=\widehat{\text{HB}O}\)(gt)
Suy ra: ∆OEB = ∆OHB (cạnh huyền, góc nhọn)
⇒ OE = OH (hai cạnh tương ứng) (1)
Xét hai tam giác vuông OHC và ODC, ta có:
\(\widehat{\text{OHC}}=\widehat{\text{ODC}}\)=90oCạnh huyền OC chung
\(\widehat{\text{HCO}}=\widehat{\text{DCO}}\)(gt)
Suy ra: ∆OHC = ∆ODC (cạnh huyền, góc nhọn)
⇒ OH = OD (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: OE = OD.
a) Xét ∆BEA và ∆CDA, ta có:
BA = CA (gt)
\(\widehat{A}\)chung
AE = AD (gt)
Suy ra: ∆BEA = ∆CDA (c.g.c)
Vậy BE = CD (hai cạnh tương ứng)
b) ∆BEA = ∆CDA (chứng minh trên)
⇒\(\widehat{\text{B1}}=\widehat{\text{C1}}\);\(\widehat{\text{E1}}=\widehat{\text{D1}}\) (hai góc tương ứng)
\(\widehat{\text{E1}}+\widehat{\text{E2}}\)=180o (hai góc kề bù)
\(\widehat{\text{D1}}+\widehat{\text{D2}}\)=180o (hai góc kề bù)
Suy ra: \(\widehat{\text{E2}}=\widehat{\text{D2}}\)
AB = AC (gt)
⇒ AE + EC = AD + DB mà AE = AD (gt) => EC = DB
Xét ∆ODB và ∆OCE, ta có:
\(\widehat{\text{E2}}=\widehat{\text{D2}}\) (chứng minh trên)
DB = EC (chứng minh trên)
\(\widehat{\text{B1}}=\widehat{\text{C1}}\)(chứng minh trên)
Suy ra: ∆ODB = ∆OEC (g.c.g)
Trả lời bởi Thảo Phương