Cho tam giác ABC vuông tại A. đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
a) Tính số đo góc ABD
b) Chứng minh : \(\Delta ABC=\Delta BAD\)
c) So sánh độ dài AM và BC
Cho tam giác ABC vuông tại A. đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
a) Tính số đo góc ABD
b) Chứng minh : \(\Delta ABC=\Delta BAD\)
c) So sánh độ dài AM và BC
Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho \(BE=\dfrac{1}{3}BC\). Gọi K là giao điểm của AE và CD.
Chứng minh rằng DK = KC
Xét ΔACD có
CB là đường trung tuyến
CE=2/3CB
Do đó: E là trọng tâm của ΔACD
=>AE là đường trung tuyến ứng với cạnh DC
=>K là trung điểm của CD
Trả lời bởi Nguyễn Lê Phước ThịnhGọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
Hướng dẫn:
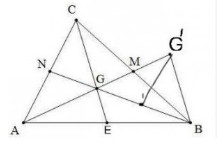
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA =  AM
AM
Mà GA = GG’ ( G là trung điểm của AG ‘)
GG’ =  AM
AM
Vì G là trọng tâm của ∆ABC => GB =  BN
BN
Mặt khác : GM =  AG ( G là trọng tâm )
AG ( G là trọng tâm )
AG = GG’ (gt)
GM =  GG’
GG’
M là trung điểm GG’
Do đó ∆GMC = ∆G’MB vì :
GM = MG’
MB = MC
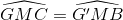
=> BG' = CG
mà CG =  CE (G là trọng tâm ∆ABC)
CE (G là trọng tâm ∆ABC)
=> BG' =  CE
CE
Vậy mỗi cạnh của ∆BGG' bằng  đường trung tuyến của ∆ABC
đường trung tuyến của ∆ABC
b) So sánh các đường trung tuyến của ∆BGG' với cạnh ∆ABC
ta có: BM là đường trung tuyến ∆BGG'
mà M là trung điểm của BC nên BM =  BC
BC
Vì IG =  BG (I là trung điểm BG)
BG (I là trung điểm BG)
GN =  BG ( G là trọng tâm)
BG ( G là trọng tâm)
=> IG = GN
Do đó ∆IGG' = ∆NGA (cgc) => IG' = AN => IG' = 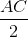
- Gọi K là trung điểm BG => GK là trung tuyến ∆BGG'
Vì GE =  GC (G là trọng tâm ∆ABC)
GC (G là trọng tâm ∆ABC)
=> GE =  BG
BG
mà K là trung điểm BG' => KG' = EG
Vì ∆GMC = ∆G'BM (chứng minh trên)
=> 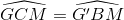 (lại góc sole trong)
(lại góc sole trong)
=> CE // BG' => 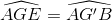 (đồng vị)
(đồng vị)
Do đó ∆AGE = ∆GG'K (cgc) => AE = GK
mà AE =  AB nên GK =
AB nên GK =  AB
AB
Vậy mỗi đường trung tuyến ∆BGG' bằng một nửa cạnh của tam giác ABC song song với nó
Trả lời bởi Thien Tu BorumCho tam giác ABC. Trên đường trung tuyến AM của tam giác đó, lấy hai điểm D, E sao cho AD = DE = EM. Gọi O là trung điểm đoạn thẳng DE. Khi đó trọng tâm của tam giác ABC là :
(A) điểm D (B) điểm E
(C) điểm O (D) cả (A), (B), (C) đều sai
Hãy chọn phương án đúng ?
Chứng minh định lí : Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau ?
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
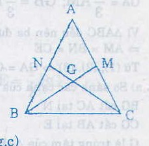
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN
Trả lời bởi Tuyết Nhi MelodyChứng minh rằng nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân ?
Gọi Δ ABC có trung tuyến BM = CN, G là trọng tâm Δ (giao điểm các trung tuyến)
Ta có :
GB = 2/3.BM
GC = 2/3.CN
Mà BM = CN => GB = GC
=> Δ BGC cân tại G
=> ∠ MBC = ∠ NCB
Xét Δ BMC và Δ CNB :
BM = CN
∠ MBC = ∠ NCB
BC là cạnh chung
=> Δ BMC = Δ CNB (c - g - c)
=> ∠ MCB = ∠ NBC
hay ∠ ACB = ∠ ABC
=> Δ ABC cân tại A (đpcm)
Cho G là trọng tâm của tam giác DEF với đường trung tuyến DH (h.24)
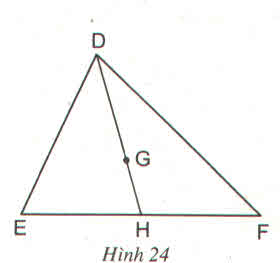
Trong các khẳng định sau đây, khẳng định nào đúng ?
\(\dfrac{DG}{DH}=\dfrac{1}{2};\dfrac{DG}{GH}=3\)
\(\dfrac{GH}{DH}=\dfrac{1}{3};\dfrac{GH}{DG}=\dfrac{2}{3}\)
G là trọng tâm của tam giác DEF với đường trung tuyến DH. Khẳng định đúng là:
vì
nên
Tức là:
Trả lời bởi Tuyết Nhi MelodyBiết rằng : Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:
Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3cm, AC = 4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC ?
∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
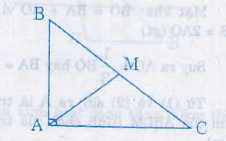
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = BC
Vì G là trọng tâm của ∆ ABC nên AG = AM => AG =. BC
=> AG = BC = .5 = 1.7cm
Trả lời bởi Tuyết Nhi MelodyGọi G là trọng tâm của tam giác đều ABC. Chứng minh rằng :
\(GA=GB=GC\)
Hướng dẫn : Áp dụng định lí ở bài tập 26 - Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau
ướng dẫn:
Gọi M, N, E là giao điểm của AG, BG, CG với BC, CA, AB.
Vì G là trọng tâm của ∆ABC nên
GA = 2323AM; GB = 2323BN; GC = 2323CE (1)
Vì ∆ABC đều nên ba đường trung tuyến ứng với ba cạnh BC, CA, AB bằng nhau
=> AM = BN = CE (2)
Từ (1), (2) => GA = GB = GC
Trả lời bởi Thien Tu BorumTheo kết quả của bài 64 chương II, phần Hình học, SBT Toán 7 một ta có :
Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
Vận dụng kết quả trên để giải bài toán sau : Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng :
a) IK // DE, IK = DE
b) \(AG=\dfrac{2}{3}AD\)
a) DE // AB, DE = \(\dfrac{1}{2}\)AB, IK // AB, IK = \(\dfrac{1}{2}\)AB
=> DE//IK và DE = IK
b) Xét tg GDE và tg GIK có:
DE = IK (cmt)
GDE = GIK (slt)
GED = GKI (slt)
=> tg GDE = tg GIK (g.c.g)
=> GD = GI ( c.t.ứ)
Có GD = GI = IA nên AG = \(\dfrac{2}{3}\)AD
Trả lời bởi ๖ۣۜDũng™♛
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
Trả lời bởi Phạm Thảo Vân