Cho hình 7.
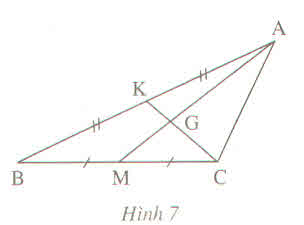
Điền vào chỗ trống :
\(GK=.....CK;AG=.....GM;GK=.....CG;AM=......AG;AM=.....GM\)
Cho hình 7.

Điền vào chỗ trống :
\(GK=.....CK;AG=.....GM;GK=.....CG;AM=......AG;AM=.....GM\)
Chứng minh rằng nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân ?
Gọi Δ ABC có trung tuyến BM = CN, G là trọng tâm Δ (giao điểm các trung tuyến)
Ta có :
GB = 2/3.BM
GC = 2/3.CN
Mà BM = CN => GB = GC
=> Δ BGC cân tại G
=> ∠ MBC = ∠ NCB
Xét Δ BMC và Δ CNB :
BM = CN
∠ MBC = ∠ NCB
BC là cạnh chung
=> Δ BMC = Δ CNB (c - g - c)
=> ∠ MCB = ∠ NBC
hay ∠ ACB = ∠ ABC
=> Δ ABC cân tại A (đpcm)
Hãy chứng minh định lí đảo của định lí trên : Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân ?
Giả sử ∆ABC có hai đường trung tuyến BM và CN gặp nhau ở G
=> G là trọng tâm của tam giác
=> GB = BM; GC = CN
mà BM = CN (giả thiết) nên GB = GC
=> ∆GBC cân tại G =>
do đó ∆BCN = ∆CBM vì:
BC là cạnh chung
CN = BM (gt)
(cmt)
=> => ∆ABC cân tại A
Trả lời bởi Tuyết Nhi MelodyGọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
Hướng dẫn:
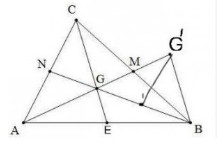
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA =  AM
AM
Mà GA = GG’ ( G là trung điểm của AG ‘)
GG’ =  AM
AM
Vì G là trọng tâm của ∆ABC => GB =  BN
BN
Mặt khác : GM =  AG ( G là trọng tâm )
AG ( G là trọng tâm )
AG = GG’ (gt)
GM =  GG’
GG’
M là trung điểm GG’
Do đó ∆GMC = ∆G’MB vì :
GM = MG’
MB = MC
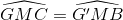
=> BG' = CG
mà CG =  CE (G là trọng tâm ∆ABC)
CE (G là trọng tâm ∆ABC)
=> BG' =  CE
CE
Vậy mỗi cạnh của ∆BGG' bằng  đường trung tuyến của ∆ABC
đường trung tuyến của ∆ABC
b) So sánh các đường trung tuyến của ∆BGG' với cạnh ∆ABC
ta có: BM là đường trung tuyến ∆BGG'
mà M là trung điểm của BC nên BM =  BC
BC
Vì IG =  BG (I là trung điểm BG)
BG (I là trung điểm BG)
GN =  BG ( G là trọng tâm)
BG ( G là trọng tâm)
=> IG = GN
Do đó ∆IGG' = ∆NGA (cgc) => IG' = AN => IG' = 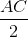
- Gọi K là trung điểm BG => GK là trung tuyến ∆BGG'
Vì GE =  GC (G là trọng tâm ∆ABC)
GC (G là trọng tâm ∆ABC)
=> GE =  BG
BG
mà K là trung điểm BG' => KG' = EG
Vì ∆GMC = ∆G'BM (chứng minh trên)
=> 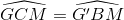 (lại góc sole trong)
(lại góc sole trong)
=> CE // BG' =>  (đồng vị)
(đồng vị)
Do đó ∆AGE = ∆GG'K (cgc) => AE = GK
mà AE =  AB nên GK =
AB nên GK =  AB
AB
Vậy mỗi đường trung tuyến ∆BGG' bằng một nửa cạnh của tam giác ABC song song với nó
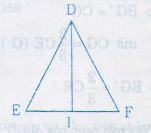
Trả lời bởi Thien Tu BorumCho tam giác DEF cân tại D với đường trung tuyến DI
a) Chứng minh \(\Delta DEI=\Delta DFI\)
b) Cho biết số đo của hai góc DIE và DIF
c) Biết DE = DF = 13 cm, EF = 10 cm. Hãy tính độ dài đường trung tuyến DI ?
a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)
b) Vì ∆DEI = ∆DFI =>
mà = 1800 ( kề bù)
nên = 900
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12
Trả lời bởi Tuyết Nhi MelodyChứng minh định lí : Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau ?
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
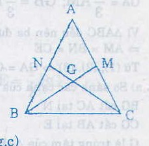
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN
Trả lời bởi Tuyết Nhi MelodyCho hình 25.
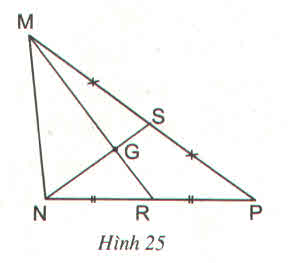
Hãy điền số thích hợp vào chỗ trống trong các đẳng thức sau
a) MG = .......MR; GR = ....MR; GR = .... MG
b) NS =........NG; NS = ........GS; NG = ......GS
Từ hình vẽ ta thấy: S, R là hai trung điểm của hai đoạn thẳng trong tam giác nên NS và MR là hai đường trung tuyến.
G là giao của hai đường trung tuyến nên G là trọng tâm của ΔMNS, do đó ta có thể điền:
Trả lời bởi Tuyết Nhi Melody
Cho G là trọng tâm của tam giác DEF với đường trung tuyến DH (h.24)
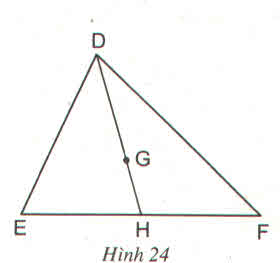
Trong các khẳng định sau đây, khẳng định nào đúng ?
\(\dfrac{DG}{DH}=\dfrac{1}{2};\dfrac{DG}{GH}=3\)
\(\dfrac{GH}{DH}=\dfrac{1}{3};\dfrac{GH}{DG}=\dfrac{2}{3}\)
G là trọng tâm của tam giác DEF với đường trung tuyến DH. Khẳng định đúng là:
vì
nên
Tức là:
Trả lời bởi Tuyết Nhi MelodyBiết rằng : Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:
Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3cm, AC = 4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC ?
∆ABC vuông tại A => BC2 = AB2 + AC2
BC2 = 32 + 42
BC2 = 25
BC = 5
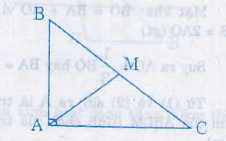
Gọi M là trung điểm của BC => AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM = BC
Vì G là trọng tâm của ∆ ABC nên AG = AM => AG =. BC
=> AG = BC = .5 = 1.7cm
Trả lời bởi Tuyết Nhi MelodyGọi G là trọng tâm của tam giác đều ABC. Chứng minh rằng :
\(GA=GB=GC\)
Hướng dẫn : Áp dụng định lí ở bài tập 26 - Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau
ướng dẫn:
Gọi M, N, E là giao điểm của AG, BG, CG với BC, CA, AB.
Vì G là trọng tâm của ∆ABC nên
GA = 2323AM; GB = 2323BN; GC = 2323CE (1)
Vì ∆ABC đều nên ba đường trung tuyến ứng với ba cạnh BC, CA, AB bằng nhau
=> AM = BN = CE (2)
Từ (1), (2) => GA = GB = GC
Trả lời bởi Thien Tu Borum
GK+1/3CK;AG=2/1GM;GK=1/2CG;AM=3/2AG;
AM=3/1GM
Trả lời bởi Vy huu Nguyen