Bài 4: Tính chất ba đường trung tuyến của tam giác

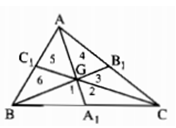
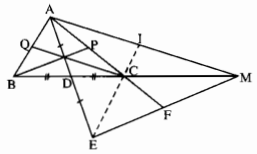
a) DE // AB, DE = \(\dfrac{1}{2}\)AB, IK // AB, IK = \(\dfrac{1}{2}\)AB

=> DE//IK và DE = IK

b) Xét tg GDE và tg GIK có:

DE = IK (cmt)

GDE = GIK (slt)

GED = GKI (slt)

=> tg GDE = tg GIK (g.c.g)

=> GD = GI ( c.t.ứ)

Có GD = GI = IA nên AG = \(\dfrac{2}{3}\)AD

Xét ΔACD có

CB là đường trung tuyến

CE=2/3CB

Do đó: E là trọng tâm của ΔACD

=>AE là đường trung tuyến ứng với cạnh DC

=>K là trung điểm của CD

Chọn B

a. Xét ΔAMC và ΔBMD, ta có:

BM = MC (gt)

∠(AMB) = ∠(BMC) (đối đỉnh)

AM = MD (gt)

Suy ra: ΔAMC = ΔDMB (c.g.c)

⇒ ∠(MAC) = ∠D (2 góc tương ứng)

Suy ra: AC // BD

(vì có 2 góc ở vị trí so le trong bằng nhau)

Mà AB ⊥ AC (gt) nên AB ⊥ BD.

Vậy (ABD) = 90^o

b. Xét ΔABC và ΔBAD ta có:

AB cạnh chung

∠(BAC) = ∠(ABD) = 90^o

AC = BD (vì ΔAMC = ΔDMB)

Suy ra: ΔABC = ΔBAD (c.g.c)

c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)

Mặt khác: AM = 1/2 AD

Vậy AM = 1/2 BC.

D

Gọi O là giao điểm của AB và CD

=>O là trung điểm chng của AB và CD

Xét ΔACD có 

AO là đường trung tuyến

CE là đường trung tuyến

AO cắt CE tại I

Do đó: I là trọng tâm

=>AI=2/3AO=1/3AB(1)

Xét ΔCBD có 

BO là đường trung tuyến

CF là đường trung tuyến

BO cắt CF tại J

Do đó; J là trọng tâm

=>BJ=2/3BO=1/3BA(2)

Từ (1) và (2) suy ra AI=BJ=1/3AB=JI

Hình vẽ:

Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6

Vì G là trọng tâm nên ta có: 

\(S_{GAB}=S_{GBC}=S_{GCA}=\dfrac{1}{3}S_{ABC}\)

Ta lại có \(S_1=S_2;S_3=S_4;S_5=S_6\) (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau, vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau)

Giải

a) Do AD = DE nên MD là một đường trung tuyến của tam giác AEM. Hơn nữa do

Nên C là trọng tâm của tam giá AEM.

b) Các đường thẳng AC, EC lần lượt cắt EM, AM tại F, I. Tam giác AEM có các đường trung tuyến là AF, EI, MD. Ta có ∆ADB = ∆EDG (c.g.c) nên AB = EC

Vậy:

c) Trước tiên, theo giả thiết, ta có AD = DE nên

Gọi BP, CQ là các trung tuyến của ∆ABC.

∆BCP = ∆MCF => . Ta sẽ chứng minh

Ta có:

Hai tam giác ACQ và CAI có cạnh AC chung, ;

nên chúng bằng nhau.

Vậy .

Tóm lại:

Xét ΔABC có các đường trung tuyến \(AA_1;BB_1\) cắt nhau tại O

nên O là trọng tâm

=>AO=2/3AA₁

\(\Leftrightarrow S_{AA_1B}=\dfrac{2}{3}S_{AOB}\)

\(\Leftrightarrow S_{ABC}=3\cdot S_{AOB}=15\left(cm^2\right)\)

Ta có: ΔMAB cân tại M

nên \(\widehat{MAB}=\widehat{B}\)

Ta có: ΔMAC cân tại M

nên \(\widehat{MAC}=\widehat{C}\)

Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

\(\Leftrightarrow2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)=180^0\)

hay \(\widehat{BAC}=90^0\)