Tìm giá trị của \(a\) và \(b\) :
a) Để hệ phương trình \(\left\{{}\begin{matrix}3ax-\left(b+1\right)y=93\\bx+4ay=-3\end{matrix}\right.\) có nghiệm là \(\left(x;y\right)=\left(1;-5\right)\).
b) Để hệ phương trình \(\left\{{}\begin{matrix}\left(a-2\right)x+5by=25\\2ax-\left(b-2\right)y=5\end{matrix}\right.\) có nghiệm là \(\left(x;y\right)=\left(3;-1\right)\).
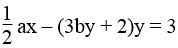 cắt nhau tại điểm M(2; -5) nên tọa độ của M là nghiệm của hệ phương trình:
cắt nhau tại điểm M(2; -5) nên tọa độ của M là nghiệm của hệ phương trình: 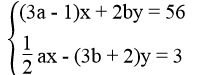
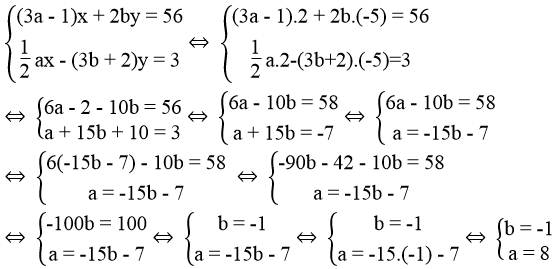






a)\(\left\{{}\begin{matrix}3ax-\left(b+1\right)y=93\\bx+4ay=-3\end{matrix}\right.\)
có nghiệm \(\left(x;y\right)=\left(1;-5\right)\) ta thay \(x=1;y=-5\) vào hệ pt trên, ta có:
\(\left\{{}\begin{matrix}3a.1-\left(b+1\right).\left(-5\right)=93\\b.1+4a.\left(-5\right)=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3a+5b+5=93\\b-20a=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3a+5b=93-5\\-\left(20a-b\right)=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3a+5b=88\\20a-b=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3a+5b=88\\100a-5b=15\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}103a=103\\3a+5b=88\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=1\\3.1+5b=88\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=1\\5b=88-3=85\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=1\\b=17\end{matrix}\right.\)
vậy để hệ pt trên có nghiệm (1;-5) thì a=1; b=17.
b) \(\left\{{}\begin{matrix}\left(a-2\right)x+5by=25\\2ax-\left(b-2\right)y=5\end{matrix}\right.\)
có nghiệm (x; y) =(3; -1), ta thay x =3; y = -1 vào pt, ta có:
\(\left\{{}\begin{matrix}\left(a-2\right).3+5b.\left(-1\right)=25\\2a.3-\left(b-2\right).\left(-1\right)=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3a-6-5b=25\\6a+b-2=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3a-5b=25+6\\6a+b=5+2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3a-5b=31\\6a+b=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6a-10b=62\\6a+b=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-11b=55\\6a+b=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-5\\6.a-5=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-5\\6a=7+5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-5\\6a=12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-5\\a=2\end{matrix}\right.\)
Vậy hệ pt trên có nghiệm (3; -1) khi a=2, b=-5.
Trả lời bởi Lê Minh Thư