Bài 1: Góc ở tâm. Số đo cung

ΔOBC cân tại O nên \(\widehat{BOC}=180^0-2\cdot\widehat{OBC}\)

ΔBO'D cân tại O' nên \(\widehat{BO'D}=180^0-2\cdot\widehat{O'BD}\)

mà \(\widehat{OBC}=\widehat{O'BD}\)

nên \(\widehat{BOC}=\widehat{BO'D}\)

Trường hợp 1: D nằm giữa A và C

=>\(\widehat{AOD}=90^0-60^0=30^0\)

=>\(\widehat{DOB}=150^0\)

Trường hợp 2: D nằm giữa B và C

ΔOCD cân tại O có CD=OC

nên ΔOCD đều

=>\(\widehat{COD}=60^0\)

hay \(\widehat{BOD}=30^0\)

a) Đúng

b) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.

c) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.

Ta có OA = AT (gt) nên \(\Delta\)AOT là tam giác vuông cân tại A, vậy \(\widehat{AOB}=45^0\)

Suy ra số đo cung nhỏ AB = 45⁰. Do đó số đo cung lớn AB bằng : \(360^0-45^0=315^0\)

từ 1 giờ đến 3 giờ thì kim giờ quay được 1 góc ở tâm 60⁰

từ 1 giờ đến 6 giờ thì kim giờ quay được 1 góc ở tâm 150⁰

a) 90 độ

b) 150 độ

c) 180 độ

d) 120 độ

e) 0 độ

Nối OA, OB

Đo góc ở tâm góc AOB để suy ra số đo góc AMB

\(\Rightarrow\) Số đo \(\widehat{AnB}\) = 360⁰ - số đo \(\widehat{AmB}\)

a) Hình a. Ta có: \(\widehat{AOB}\)=125⁰

\(\Rightarrow\) Số đo cung AmB = 125⁰ và số đo góc \(\widehat{AnB}\) = 360⁰ - 125⁰ = 235⁰

b) Hình b. Ta có \(\widehat{AOB}\) = 65⁰

\(\Rightarrow\)Số đo cung AmB = 65⁰ và số đo \(\widehat{AnB}\) = 360⁰ - số đo cung AmB = 360⁰ - 65⁰ = 295⁰

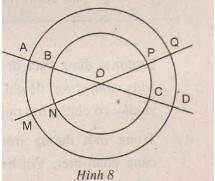
a) các cung nhỏ AM, CP, BN, DQ có cùng số đo

b) cung AM = DQ; cung BN = PC; cung AQ = MD; cung BP = NC.

c) các cung lớn bằng nhau: AQDM = DMAQ; BPCN = PBNC; AMDQ = MAQD; BNCP = NBPC; AQD = AMD = MAQ = MDQ BPC = BNC = NBP = NCP