Cho hình thang cân \(ABCD\) có hai đáy \(AB< CD\). Chọn khẳng định đúng?
\(BD^2-BC^2=CD.AB.\)\(BD^2-BC^2=AB^2.\)\(BD^2-BC^2=2CD.AB.\)\(BD^2-BC^2=BC.AD.\)Hướng dẫn giải: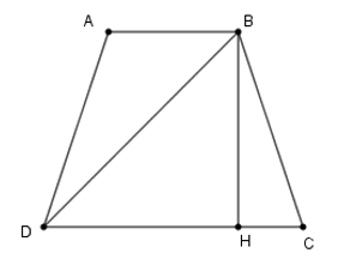
Kẻ \(BH\perp CD\).
Áp dụng định lí Pytago ta có: \(BD^2=BH^2+DH^2;BC^2=BH^2+CH^2\)
\(\Rightarrow BD^2-BC^2=DH^2-CH^2=\left(DH+CH\right)\left(DH-CH\right)=CD.AB.\) (Vì ta dễ dàng chứng minh được \(DH=AB+CH\)).
