Bài tập cuối chương V

1. Khái niệm phân số

• \(\dfrac{a}{b}\) là phân số nếu \(a, b\in \mathbb{Z}\), \(b\) ≠ 0.
• a gọi là tử số (hay là tử), b gọi là mẫu số (hay là mẫu).

2. Quy tắc bằng nhau của hai phân số

• Nếu \(\dfrac{a}{b}=\dfrac{c}{d}\) thì \(a.d=b.c\). Ngược lại, nếu \(a.d=b.c\) thì \(\dfrac{a}{b}=\dfrac{c}{d}.\)
• Với \(a, b \in \mathbb{Z}\), \(b\) ≠ 0 thì ta luôn có: \(\dfrac{a}{-b}=\dfrac{-a}{b};\dfrac{-a}{-b}=\dfrac{a}{b}.\)

Ví dụ. Hai phân số \(-\dfrac{3}{5}\) và \(\dfrac{6}{-10}\) bằng nhau vì \(-\dfrac{3}{5}=\dfrac{-3}{5};\left(-3\right).\left(-10\right)=5.6\).

3. Tính chất cơ bản của phân số

• \(\dfrac{a}{b}=\dfrac{a\cdot m}{b\cdot m}\) với \(m \in \mathbb{Z}\), \(m\) ≠ 0.
• \(\dfrac{a}{b}=\dfrac{a:n}{b:n}\) với \(n \in\) ƯCLN (a; b).

Ví dụ.

1) \(\dfrac{-30}{72}=\dfrac{\left(-30\right):3}{72:3}=\dfrac{-10}{24}.\)

2) \(\dfrac{2}{5}=\dfrac{2.5}{5.5}=\dfrac{10}{25}\).

4. Rút gọn về phân số tối giản

Phân số tối giản là phân số mà tử và mẫu chỉ có ước chung là 1 và -1. 

Ví dụ: \(\dfrac{10}{21};\dfrac{3}{5};\dfrac{-5}{9}\) là các phân số tối giản.

Để rút gọn phân số về phân số tối giản ta thường làm như sau:

Bước 1. Tìm ƯCLN của tử và mẫu sau khi đã bỏ đi dấu " - " (nếu có)

Bước 2. Chia cả tử và mẫu cho ƯCLN vừa tìm được, ta có phân số tối giản cần tìm.

Ví dụ. Rút gọn phân số \(\dfrac{36}{81}\) về phân số tối giản.

ƯCLN (36; 81) = 9; \(\dfrac{36}{81}=\dfrac{36:9}{81:9}=\dfrac{4}{9}\).

5. Hỗn số dương

Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 (với tử và mẫu dương) rồi viết chúng liền nhau thì được một hỗn số dương.

Ví dụ. \(\dfrac{13}{4}=\dfrac{3.4+1}{4}=3+\dfrac{1}{4}=3\dfrac{1}{4}.\)

6. Cộng, trừ hai phân số

a) Cộng, trừ hai phân số cùng mẫu

• Muốn cộng hai phân số có cùng mẫu, ta cộng các tử và giữ nguyên mẫu.

\(\dfrac{a}{m}+\dfrac{b}{m}=\dfrac{a+b}{m}.\)

• Muốn trừ hai phân số có cùng mẫu, ta trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu. 

\(\dfrac{a}{m}-\dfrac{b}{m}=\dfrac{a-b}{m}.\)

b) Cộng, trừ hai phân số không cùng mẫu

Muốn cộng (trừ) hai phân số không cùng mẫu, ta quy đồng mẫu của những phân số đó rồi cộng (trừ) các tử và giữ nguyên mẫu chung. 

Ví dụ. Thực hiện các phép tính.

• \(\dfrac{5}{6}+\dfrac{3}{4}=\dfrac{5.2}{6.2}+\dfrac{3.3}{4.3}=\dfrac{10}{12}+\dfrac{9}{12}=\dfrac{19}{12}.\)
• \(\dfrac{7}{6}-\dfrac{3}{5}=\dfrac{7.5}{6.5}-\dfrac{3.6}{5.6}=\dfrac{7.5}{6.5}-\dfrac{3.6}{5.6}=\dfrac{35}{30}-\dfrac{18}{30}=\dfrac{17}{30}.\)

7. Phép nhân, phép chia phân số

• Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau.

\(\dfrac{a}{b}.\dfrac{c}{d}=\dfrac{a.c}{b.d}\) với \(b\ne0\) và \(d\ne0.\)

Ví dụ. \(\dfrac{3}{5}\cdot\dfrac{8}{15}=\dfrac{3.8}{5.15}=\dfrac{24}{75}=\dfrac{8}{15}.\)

• Phân số \(\dfrac{b}{a}\) gọi là phân số nghịch đảo của phân số \(\dfrac{a}{b}\) với \(a\ne0\) và \(b\ne0.\)
• Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia:

\(\dfrac{a}{b}:\dfrac{c}{d}=\dfrac{a}{b}.\dfrac{d}{c}=\dfrac{a.d}{b.c}\) với \(b,c,d\) khác 0.

Ví dụ. \(\dfrac{12}{5}:\dfrac{-4}{3}=\dfrac{12}{5}\cdot\dfrac{3}{-4}=\dfrac{36}{-20}=\dfrac{9}{-5}.\)

Nhận xét: Nói chung, các phép tính cộng, trừ, nhân, chia phân số có các tính chất giống như trong tập hợp số nguyên: giao hoán, kết hợp, cộng với số 0, nhân với số 1, tính chất phân phối của phép nhân đối với phép tính cộng và trừ.

8. Các phép tính đối với số thập phân

Số thập phân cũng có các phép tính cộng, trừ, nhân, chia như trong phân số.

a) Phép cộng, phép trừ số thập phân

Để cộng, trừ hai số thập phân dương ta làm như sau:

Bước 1. Viết số này ở dưới số kia sao cho các chữ số ở cùng hàng đặt thẳng cột với nhau, dấu "," đặt thẳng cột với nhau.

Bước 2. Thực hiện phép cộng, trừ như phép cộng, trừ các số tự nhiên.

Bước 3. Viết dấu "," ở kết quả thẳng cột với các dấu "," đã viết ở trên.

Ví dụ. Tính 98,26 + 1,254.

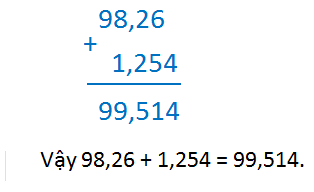
• Quy tắc cộng hai số thập phân (cùng dấu hoặc khác dấu) được thực hiện giống quy tắc cộng hai số nguyên.
• Giống như phép cộng số nguyên, phép cộng số thập phân cũng có các tính chất: giao hoán, kết hợp, cộng với số 0, cộng với số đối.
• Quy tắc dấu ngoặc đối với số thập phân giống như quy tắc dấu ngoặc đối với số nguyên

Ví dụ. Tính  (-12,45) + (80,5 - 287,55).

Ta có: (-12,45) + (80 - 287,55) = -12,45 + 80 - 287,55 = 80 - 12,45 - 287,55 = 80 - (12,45 + 287,55) = 80 - 300 = -220.

b) Phép nhân, phép chia số thập phân

Ở tiểu học ta đã biết cách tính nhân, chia số thập phân.

9. Tỉ số của hai số

Tỉ số của a và b (b ≠ 0) là thương trong phép chia số a cho số b, kí hiệu là \(a:b\) hoặc \(\dfrac{a}{b}\).

10. Tỉ số phần trăm của hai số

• Tỉ số phần trăm của a và b là \(\dfrac{a}{b}.100\%\).
• Để tính tỉ số phần trăm của a và b, ta làm như sau:

Bước 1. Viết tỉ số \(\dfrac{a}{b}\)

Bước 2. Tính số \(\dfrac{a.100}{b}\) và viết thêm % vào bên phải số vừa nhận được.

Ví dụ. Tỉ số phần trăm của 24,5 và 70 là \(\dfrac{24,5}{70}.100\%=35\%.\)

11. Tìm giá trị phân số của một số cho trước

• Muốn tìm giá trị \(\dfrac{m}{n}\) của số a cho trước, ta tính \(a\cdot\dfrac{m}{n}\) (m ∈ \(\mathbb{N}\), n ∈ \(\mathbb{N^*}\)).
• Giá trị m% của số a là giá trị phân số \(\dfrac{m}{100}\) của số a.
• Muốn tìm giá trị m% của số a cho trước, ta tính \(a\cdot\dfrac{m}{100}\) (\(m\) ∈ \(\mathbb{N^*}\)).

 Ví dụ.

a) \(\dfrac{2}{5}\) của 80 là \(\dfrac{2}{5}.80=\dfrac{2.80}{5}=36.\)

b) 42% của 270 là \(42\%\cdot270=\dfrac{42}{100}.270=\dfrac{42.270}{100}=113,4.\)

12. Tìm một số biết giá trị một phân số của số đó

• Muốn tìm một số biết \(\dfrac{m}{n}\) của số đó bằng \(a\), ta tính \(a:\dfrac{m}{n}\) (\(m, n \in \mathbb{N^*}\)).
• Muốn tìm một số biết m% của số đó bằng a, ta tính \(a:\dfrac{m}{100}\) (\(m\in\mathbb{N^*}\)).

Ví dụ. 

a) \(\dfrac{3}{8}\) của một số là 135. Số đó là: \(135:\dfrac{3}{8}=135\cdot\dfrac{8}{3}=360\).

b) 20% của một số là 45. Số đó là: \(45:20\%=45:\dfrac{20}{100}=45\cdot\dfrac{100}{20}=225.\)