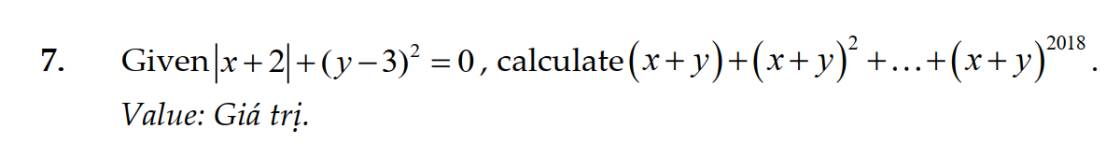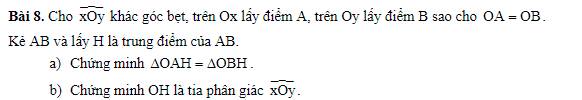
Violympic toán 7

a: Xét ΔOAH và ΔOBH có

OA=OB

AH=BH

OH chung

Do đó: ΔOAH=ΔOBH

b: Ta có: ΔOAH=ΔOBH

=>\(\widehat{AOH}=\widehat{BOH}\)

=>\(\widehat{xOH}=\widehat{yOH}\)

=>OH là phân giác của góc xOy

\(\dfrac{2x-1}{3}=\dfrac{1}{4}\)

=>\(2x-1=3\cdot\dfrac{1}{4}=\dfrac{3}{4}\)

=>\(2x=\dfrac{3}{4}+1=\dfrac{7}{4}\)

=>\(x=\dfrac{7}{4}:2=\dfrac{7}{4\cdot2}=\dfrac{7}{8}\)

phương trình bậc hai với hai biến x và y. Ta có thể giải nó bằng cách đặt (y = 5\cos{\theta}) (vì (|y| \leq 5)), từ đó suy ra (x = 2016 + \frac{5}{2}\tan{\theta}). Vì (x, y \in Z) nên (\tan{\theta}) phải là một số hữu tỉ. Ta có thể tìm các giá trị của (\theta) sao cho (\tan{\theta}) là một số hữu tỉ, từ đó suy ra các giá trị tương ứng của (x) và (y).

|x + 2| + (y - 3)² = 0

⇒ |x - 2| = 0 và (y - 3)² = 0

*) |x - 2| = 0

x - 2 = 0

x = 2

*) (y - 3)² = 0

y - 3 = 0

y = 3

x + y = 2 + (-3) = -1

(x + y) + (x + y)² + ... + (x + y)²⁰¹⁸

= -1 + (-1)² + (-1)³ + (-1)⁴ + ... + (-1)²⁰¹⁷ + (-1)²⁰¹⁸

= -1 + 1 - 1 + 1 + ... -1 + 1

= 0 + 0 + ... + 0

= 0

Lời giải:

$\frac{x+2}{2020}+\frac{x+2}{2020}=\frac{x+2019}{3}+\frac{x+2020}{2}$

$\frac{x+2}{2020}+1+\frac{x+2}{2020}+2=\frac{x+2019}{3}+1+\frac{x+2020}{2}+1$

$\frac{x+2022}{2020}+\frac{x+2022}{2020}=\frac{x+2022}{3}+\frac{x+2022}{2}$

$(x+2022)(\frac{1}{2020}+\frac{1}{2020}-\frac{1}{3}-\frac{1}{2})=0$

Dễ thấy $\frac{1}{2020}+\frac{1}{2020}-\frac{1}{3}-\frac{1}{2}<0$

Do đó: $x+2022=0$

$\Rightarrow x=-2022$

help

1 - 2x = -(2x - 1) 

= -(2x + 6 - 7)

= -(2x + 6) + 7

= -2(x + 3) + 7

Để B nguyên thì (1 - 2x) ⋮ (x + 3)

⇒ 7 ⋮ (x + 3)

⇒ x + 3 ∈ Ư(7) = {-7; -1; 1; 7}

⇒ x ∈ {-10; -4; -2; 4}

|2x - 1| + (y - 2)² ≤ 0 (1)

Do |2x - 1| ≥ 0 và (y - 2)²⁰²² ≥ 0 (với mọi x, y ∈ R)

(1) ⇒  |2x - 1| + (y - 2)²⁰²² = 0

⇒ |2x - 1| = 0 và (y - 2)²⁰²² = 0

*) |2x - 1| = 0

2x - 1 = 0

2x = 1

x = 1/2

*) (y - 2)²⁰²² = 0

y - 2 = 0

y = 2

⇒ B = 12x² + 4xy²

= 12.(1/2)² + 4.(1/2).2²

= 3 + 8

= 11

Bạn cần giải thích bài nào nhỉ?