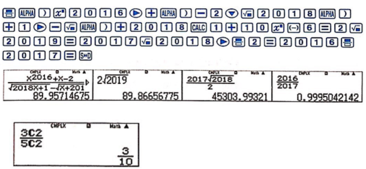
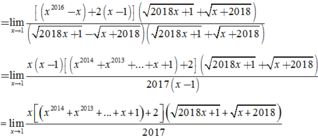X2016 = 3X2015 . Tìm X
PA
Những câu hỏi liên quan
cho x1,..x2016 thỏa mãn:1/x1^2+...+1/x2016^2=1CM trong các số từ x1->x2016 có ít nhất 2 số bằng nhau
Một bạn nhờ mình đăng hộ ( phan thuy anh )
Tìm N(2017) biết đa thức N(x)=x2017−2018.x2016+2018.x2015−2018.x2014+........−2018.x2+2018.x−1
Giải bất phương trình
2017
-
x
2016
+
2016
-
x
2017
≤
1
. Gọi tập nghiệm là S. Tìm S A.
2016
;
2017
B. ...
Đọc tiếp
Giải bất phương trình 2017 - x 2016 + 2016 - x 2017 ≤ 1 . Gọi tập nghiệm là S. Tìm S
A. 2016 ; 2017
B. ( - ∞ , 2016 ] ∪ [ 2017 , + ∞ )
C. 2016 , 2017
D. S=R
tính nhanh 2016 x2016 - 2000 x 2032 = ?
2016 x 2016-2000 x 2032
=2016 x (2000+16)-2000 x (2016+16)
=2016 x 2000+2016 x 16-2000 x 2016-2000 x 16
=2016 x 16-2000 x 16
=(2016-2000) x 16
=16 x 16
=256
Đúng 0
Bình luận (0)
2016 x 2016 - 2000 x 2032
= 2016 x 2016 - 2000 x ( 2016 + 16 )
= 2016 x 2016 - 2000 x 2016 - 2000 x 16
= 2016 x ( 2016 - 2000 ) - 2000 x 16
= 2016 x 16 - 2000 x 16
= 16 x ( 2016 - 2000 )
= 16 x 16
= 256
Cấm ai chép nhé
= 64000 + 256
= 64256
Đúng 0
Bình luận (0)
2016 x 2016 - 2000 x 2032 = 2016 x 2016 - (2016 - 16) x (2016 + 16) = 2016 x 2016 - (2016 x 2016 - 16 x 16)
= 2016 x 2016 - 2016 x 2016 + 16 x 16 = 256
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm hệ số của số hạng chứa
x
3
trong khai triển
1
-
2
x
+
2015
.
x
2016
-
2016
.
x...
Đọc tiếp
Tìm hệ số của số hạng chứa x 3 trong khai triển
1 - 2 x + 2015 . x 2016 - 2016 . x 2017 + 2017 . x 2018 60
A. - C 60 3
B. C 60 3
C. 8 . C 60 3
D. - 8 . C 60 3
hoi so a = 1 x 2 x 3 x ..........x2016 co tan cung bao nhieu chu so 0
theo cảm tính là 5
Tìm đáp án sau biết đáp án là số tự nhiên
5/4x6/5x7/6....x2016/2015
5/4x6/5x7/6x...x2016/2015
=5x6x7x...x2016/4x5x6x...x2015=2016/4=504
Tick nhé
Đúng 0
Bình luận (0)
Xác định giá trị thực k để hàm số
f
x
x
2016
+
x
-
2
2018
x
+
1...
Đọc tiếp
Xác định giá trị thực k để hàm số f x = x 2016 + x - 2 2018 x + 1 - x + 2018 , x ≠ 1 k , x = 1 liên tục tại x = 1.
A. k = 1
B. k = 2 2019
C. k = 2017 . 2018 2
D. 20016 2017 2019
Đáp án B
Để f(x) liên tục tại x = 1 thì lim x → 1 f ( x ) = f ( 1 ) . Ta có:
lim x → 1 f ( x ) = l i m x 2016 + x - 1 2018 x + 1 - x + 2018 = lim x → 1 2016 x + 1 1009 2018 x + 1 - 1 2 x + 2018 = 2 2019
Vậy k = 2 2019 .
Đúng 0
Bình luận (0)
Xác định giá trị thực k để hàm số
f
x
x
2016
+
x
−
2
2018
x
+
1...
Đọc tiếp
Xác định giá trị thực k để hàm số f x = x 2016 + x − 2 2018 x + 1 − x + 2018 khi x ≠ 1 k khi x = 1 liên tục tại điểm x=1
A. k = 1.
B. k = 2 2019 .
C. k = 2017 2018 2 .
D. 2016 2017 .
Xác định giá trị thực k để hàm số
f
x
x
2016
+
x
−
2
2018
x
+
1
−...
Đọc tiếp
Xác định giá trị thực k để hàm số f x = x 2016 + x − 2 2018 x + 1 − x + 2018 khi x ≠ 1 k khi x = 1 liên tục tại điểm x = 1
A. k = 1.
B. k = 2 2019 .
C. k = 2017 2018 2 .
D. k = 2016 2017 .
Đáp án B
Cách1: Tư duy tự luận
Hàm số liên tục tại điểm x = 1 khi lim x → 1 f x = f 1 .
Ta có f 1 = k và lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 .
= lim x → 1 x 2016 − x + 2 x − 1 2018 x + 1 + x + 2018 2018 x + 1 − x + 2018 2018 x + 1 + x + 2018
= lim x → 1 x x − 1 x 2014 + x 2013 + ... + x + 1 + 2 2018 x + 1 + x + 2018 2017 x − 1
= lim x → 1 x x 2014 + x 2013 + ... + x + 1 + 2 2018 x + 1 + x + 2018 2017 = 2015 + 2 .2 1019 2017
= 2 2019
Vậy để hàm số liên tục tại điểm x=1 khi k = 2 2019
Cách 2: Tư duy tự luận (tính giới hạn bằng công thức L’Hospital)
Ta có
lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 = lim x → 1 2016 x 2015 + 1 1009 2018 x + 1 − 1 2 x + 2018
= 2016 + 1 1009 2019 − 1 2 2019 = 2 2019
Hàm số liên tục tại điểm x=1 khi lim x → 1 f x = f 1 ⇔ k = 2 2019 .
Cách 3: Sử dụng máy tính cầm tay (casio và vinacal)
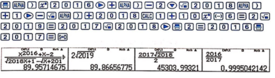
lim x → 1 f x = lim x → 1 x 2016 + x − 2 2018 x + 1 − x + 2018 = 2 2019 .
Hàm số liên tục tại điểm x=1 khi lim x → 1 f x = f 1 ⇔ k = 2 2019 .
Đúng 0
Bình luận (0)