cho các cặp số thực (x;y) thỏa mãn :\(\frac{x^2-x+y^2-y}{x^2+y^2-1}\le0\)
Hãy tìm cắp số có tổng \(x+2y\)lớn nhất
tìm tất cả các cặp số thực (x;y) sao cho y là số nhỏ nhất thoả mãn điều kiện \(x^2+5y^2+2y+4xy-3=0\)
\(x^2+5y^2+2y+4xy-3=0\)
\(\Leftrightarrow\)\((x^2+4xy+4y^2)+(y^2+2y+1)=4\)
\(\Leftrightarrow\)\((x+2y)^2+(y+1)^2=4\)
\(\Leftrightarrow\)\((x+2y)^2=4-(y+1)^2\)
\(\Leftrightarrow\)\((x+2y)^2=(2-y-1)(2+y+1)\)
\(\Leftrightarrow\)\((x+2y)^2=(1-y)(3+y)\)
\(Vì \) \((x+2y)^2\geq0\)
\(\Rightarrow\)\((1-y)(3+y)\geq0\)
\(\Rightarrow\)\(\left[\begin{array}{}
\begin{cases}
1-y\geq0\\
3+y\geq0
\end{cases}\\
\begin{cases}
1-y\leq0\\
3+y\leq0
\end{cases}
\end{array} \right.\)
\(\Rightarrow\)\(\left[\begin{array}{}
\begin{cases}
y\leq1\\
y\geq-3
\end{cases}\\
\begin{cases}
y\geq1\text{(Vô lí)}\\
y\leq-3\text{(Vô lí)}
\end{cases}
\end{array} \right.\)\(\Rightarrow\)\(-3\leq y\leq1\)
\(\text{Mà y là số nhỏ nhất}\)
\(\Rightarrow\)\(y=-3\)
\(\Rightarrow\)\(x+2.(-3)=0\text{ (Vì }(x+2y)^2\geq0)\)
\(\Rightarrow\)\(x=6\)
\(\text{Vậy cặp số (x,y) thỏa mãn yêu cầu bài toán là: (6;-3)}\)
Nếu mình đúng cho mình xin 1 like nha
Biết rằng x; y là các số thực sao cho các số x; 2x- 3; y theo thứ tự lập thành một cấp số cộng và các số x 2 ; xy − 6 y ; y 2 theo thứ tự lập thành một cấp số nhân. Cặp số (x;y) là
A. 7 ; 3 7 và − 7 ; − 3 7
B. - 7 ; 3 7 và 7 ; − 3 7
C. 2 ; 3 2 và − 2 ; − 3 2
D. - 2 ; 3 7 và 2 ; 3 7
Tìm các cặp số thực (x;y) sao cho x và y thỏa mãn đồng thời hai điều kiện: x=x^2+y^2; y=2xy.
Tìm các cặp số thực(x;y)sao cho x và y thỏa mãn đồng thời hai điều kiện: x=x mũ2+y mũ2 và y=2xy
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ 1 , giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x 2 + y 2 + 4 x + 6 y + 13 - m = 0 thuộc tập nào sau đây?
A. [8;10]
B. [5;7]
C. [1;4]
D. [-3;0]
Đáp án A
Ta có, giả thiết log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính R 1 = 2
Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m là đường tròn tâm I(-2;-3); R 2 = m
Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 ( 2 x + 2 y + 5 ) ≥ 1 giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m = 0 thuộc tập nào sau đây?
![]()
![]()
![]()
![]()
Đáp án A
Ta có, giả thiết
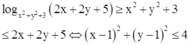
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và

Tìm các cặp số thực a và b sao cho mỗi cặp vecto sau bằng nhau:
a) \(\overrightarrow u = \left( {2a - 1; - 3} \right)\) và \(\overrightarrow v = \left( {3;4b + 1} \right)\)
b) \(\overrightarrow x = \left( {a + b; - 2a + 3b} \right)\) và \(\overrightarrow y = \left( {2a - 3;4b} \right)\)
a) Để \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}2a - 1 = 3\\ - 3 = 4b + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 1\end{array} \right.\)
Vậy \(\left\{ \begin{array}{l}a = 2\\b = - 1\end{array} \right.\) thì \(\overrightarrow u = \overrightarrow v \)
b) \(\overrightarrow x = \overrightarrow y \Leftrightarrow \left\{ \begin{array}{l}a + b = 2a - 3\\ - 2a + 3b = 4b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\end{array} \right.\)
Vậy \(\left\{ \begin{array}{l}a = 1\\b = - 2\end{array} \right.\) thì \(\overrightarrow x = \overrightarrow y \)
Cho các số thực x y z thỏa mãn.Có bao nhiêu giá trị nguyên của z để có đúng 2 cặp (x;y) thỏa mãn đẳng thức trên:
A.2
B.211
C.99
D.4
Cho X = {-1; 0; 1; 2}, f là 1 quan hệ từ tập hơn X đến tập hơn số thực R được xác định bởi các cặp giá trị tương ứng sau:
| x | 0 | 1 | 2 | -1 | 0 |
| f(x) | 1 | 0 | 1 | 1 | 2 |
f có phải là một hàm số không? Giải thích.