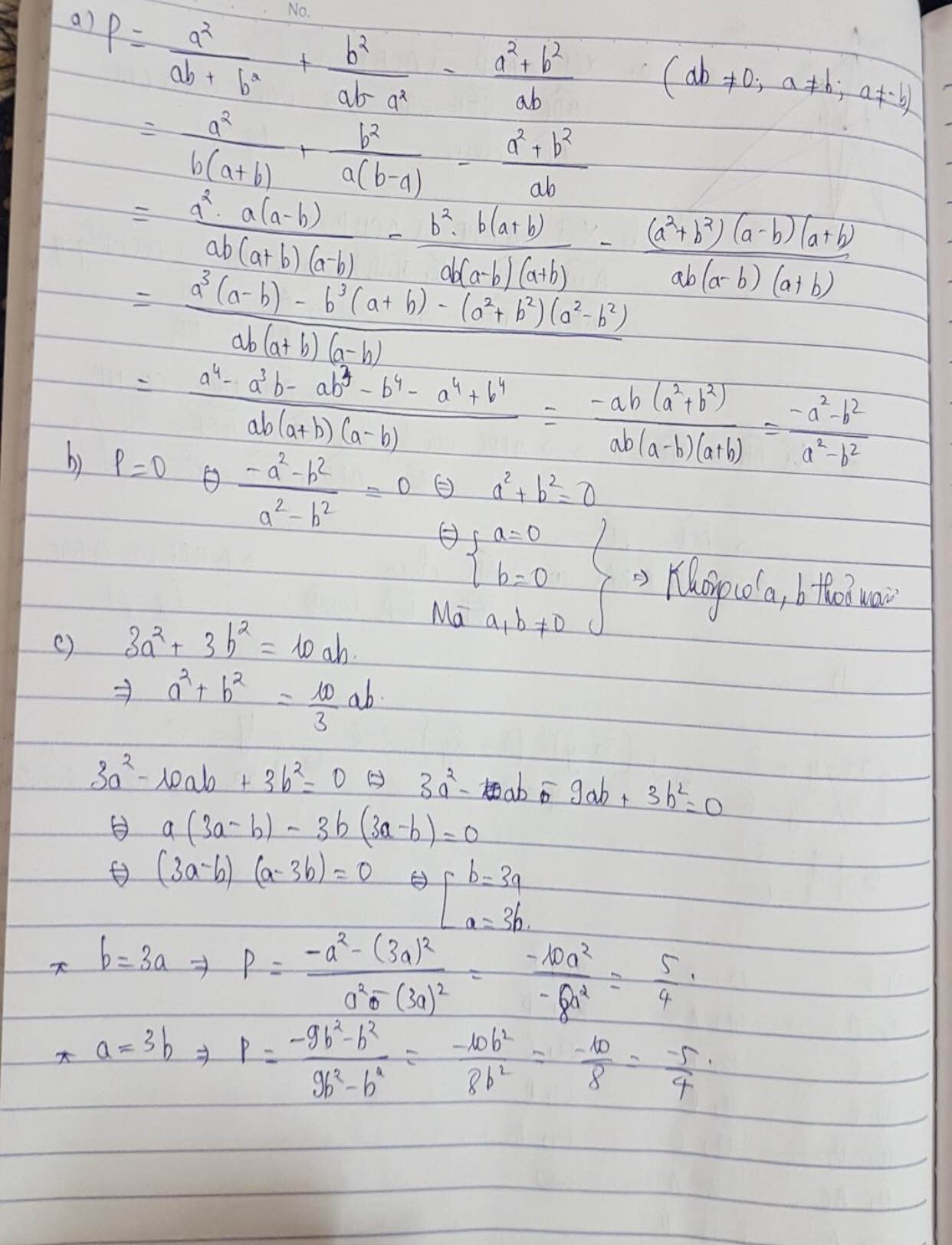Cho 3a2+3b2=10ab và b>a>0.Tìm giá trị biểu thức P=\(\frac{a-b}{a+b}\)
PN
Những câu hỏi liên quan
Cho 3 a 2 + 3 b 2 = 10 a b và b > a > 0. Tính giá trị của biểu thức P = a - b a + b
Cho biểu thức:
P=\(\dfrac{a^2}{ab+b^2}+\dfrac{b^2}{ab-a^2}-\dfrac{a^2+b^2}{ab}\)
a) rút gọn P
b) có giá trị nào của a,b để P=0
c) tính giá trị của P biết a,b thỏa mãn điều kiện: 3a2+3b2= 10ab và a>b>0
\(P=\dfrac{a^2}{ab+b^2}+\dfrac{b^2}{ab-a^2}-\dfrac{a^2+b^2}{ab}\) (\(a\ne b;a\ne0;a\ne-b;b\ne0\))
\(=\dfrac{a^2}{b\left(a+b\right)}+\dfrac{b^2}{a\left(b-a\right)}-\dfrac{a^2+b^2}{ab}\)
\(=\dfrac{a^3\left(a-b\right)-b^3\left(a+b\right)-\left(a^2+b^2\right)\left(a+b\right)\left(a-b\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{a^4-a^3b-b^3a-b^4-\left(a^2+b^2\right)\left(a^2-b^2\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{a^4-a^3b-b^3a-b^4-\left(a^4-b^4\right)}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{-a^3b-b^3a}{ab\left(a+b\right)\left(a-b\right)}\)
\(=\dfrac{-ab\left(a^2+b^2\right)}{ab\left(a+b\right)\left(a-b\right)}=-\dfrac{a^2+b^2}{a^2-b^2}\).
b) -Ta có: \(P=0\)
\(\Leftrightarrow-\dfrac{a^2+b^2}{a^2-b^2}=0\)
\(\Leftrightarrow a^2+b^2=0\)
-Vì \(a^2\ge0;b^2\ge0\)
\(\Rightarrow a=0;b=0\) (không thỏa mãn điều kiện).
-Vậy không có giá trị nào của a,b để \(P=0\).
c)
Đúng 1
Bình luận (0)
cho 3a2+3b2=10ab và b>a>0 . tìm giá trị của biểu thức \(P=\frac{a-b}{a+b}\)
từ 3a2+3b2=10ab\(\Rightarrow\)P^2=\(\frac{\left(a-b\right)^2}{\left(a+b\right)^2}=\frac{a^2-2ab+b^2}{a^2+2ab+b^2}=\frac{3a^2+3b^2-6ab}{3a^2+3b^2+6ab}=\frac{10ab-6ab}{10ab+6ab}=\frac{4ab}{16ab}=\frac{1}{4}\)\(\Rightarrow\)P^2=1/4
mặt khác b>a>0\(\Rightarrow\)P<0\(\Rightarrow\)P=-1/2
Đúng 0
Bình luận (0)
cho: \(3a^2+3b^2=10ab\) và \(b>a>0\)
tìm giá trị của biểu thức :
\(P=\frac{a-b}{a+b}\)
từ \(3a^2+3b^2=10ab\)
\(\Rightarrow3a^2-9ab-ab+3b^2=0\)
\(\Rightarrow3a\left(a-3b\right)-b\left(a-3b\right)=0\)
\(\Rightarrow\left(a-3b\right)\left(3a-b\right)=0\)
truường hợp a-3b=0 tức a=3b ( ko thỏa mãn đk 0<a<b<3ab)
Vậy 3a-b=0 tức là b=3a. thay vào P ta có:
\(\frac{a-b}{a+b}=\frac{a-3a}{a+3a}=\frac{-2a}{4a}=\frac{-1}{2}\) ( vì a khác 0)
Đúng 0
Bình luận (0)
Cho a>b>0 thỏa mãn \(3a^2+3b^2=10ab\)Tìm giá trị biểu thức \(P=\frac{a-b}{a+b}\)
Giúp pain đi
Ta có :
3a2 + 3b2 = 10ab
<=> 3a2 + 3b2 - 10ab = 0
<=>4a2 - a2 + 4b2 - b2 - 8ab- 2ab = 0
<=> ( 4a2 - 8ab + 4b2 ) - ( a2 + 2ab + b2 ) = 0
<=> ( 2a + 2b )2 - ( a - b )2 = 0
<=> ( 2a + 2b )2 = ( a - b )2
<=> 2a + 2b = a - b ( 1 )
Thay (1) vào P ta được :
\(P=\frac{2a+2b}{a+b}\)
\(P=\frac{2\left(a+b\right)}{a+b}\)
\(P=2\)
Đúng 0
Bình luận (0)
Mạo danh cũng ko xong , chúa pain ko bao giờ nói " giúp pain đi " hay đúng hơn là t ko cần con người giải giúp mấy bài toán easy ntn này
Đúng 0
Bình luận (0)
\(\)\(3a^2+3b^2=10ab\Rightarrow3a^2-10ab+3b^2=0.\)
\(\Leftrightarrow3ab-9ab-ab+3b^2=0\)
\(\Rightarrow3a\left(a-3b\right)-b\left(a-3b\right)=0\Rightarrow\left(3a-b\right)\left(a-3b\right)=0\)
\(\Rightarrow3a=b\)hoặc \(3b=a\)mà \(a>b\Rightarrow3b=a\)
Thay \(3b=a\)ta có :
\(P=\frac{a-b}{a+b}=\frac{3b-b}{3b+b}=\frac{2b}{4b}=\frac{1}{2}.\)
Vậy giá trih của biểu thức \(P=\frac{1}{2}.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 3a2 + 3b2 = 10ab và b > a > 0 .
Tính giá trị của biểu thức \(P=\frac{a-b}{a+b}\)
Vì \(b>a>0\Rightarrow P=\frac{a-b}{a+b}< 0\)
Ta có : \(P^2=\frac{\left(a-b\right)^2}{\left(a+b\right)^2}=\frac{a^2-2ab+b^2}{a^2+2ab+b^2}=\frac{3a^2+3b^2-6ab}{3a^2+3b^2+6ab}=\frac{10ab-6ab}{10ab+6ab}=\frac{4}{16}\)
\(\Rightarrow\orbr{\begin{cases}P=-\frac{1}{2}\\P=\frac{1}{2}\end{cases}}\) Mà P < 0 nên \(P=-\frac{1}{2}\)
Vậy \(P=\frac{a-b}{a+b}=-\frac{1}{2}\)
Đúng 0
Bình luận (0)
Sao cách em làm ra kết quả khác ah Hùng ạ:Câu hỏi của Phan Thị Hồng Nhung - Toán lớp 9
Đúng 0
Bình luận (0)
Cho a>b>0 và \(3a^2+3b^2=10ab\). Tính giá trị của biểu thức \(P=\frac{a-b}{a+b}\)
Để sử dụng đc \(a^2+b^2=\frac{10ab}{3}\) cần có \(P^2=\left(\frac{a-b}{a+b}\right)^2\)
Từ đó ta có lời giải bài toán làm tiếp đi nhé
Đúng 0
Bình luận (0)
cho a>b>0 và 3a2+3b2=10ab. Tính giá trị biểu thức P = (a-b)/(a+b)
Ta có:
\(3a^2+3b^2=10ab\Leftrightarrow\left(3a-b\right)\left(a-3b\right)=0\Rightarrow a=3b\)
Đúng 0
Bình luận (0)
cho a và b lần lượt thỏa mãn các hệ thức sau
a3-3a2+5a-2020=0 và b3-3b2=5b=2014
tính a+b