Cho △ABC nhọn , vẽ đường cao BD và CE
1) BEDC thuộc 1 đường tròn
2) CMR: DE < BC
YA
Những câu hỏi liên quan
Tam giác ABC nhọn, góc A = 60 độ, vẽ đường cao BD và CE. CMR: DE = 1/2 BC
Cho tam giác nhọn ABC nội tiếp đường tròn (O),đường cao BD,CE(D thuộc AC,E thuộc AB) cắt nhau tại H.
a)CMR: AEHD và BEDC là tứ giác nội tiếp
b)Cho Ax là tiếp tuyến tại A của (O).CMR: Ax//DE
c)Cho BK là đường kính của (O),hạ CP vuông góc BK(P thuộc BK).CMR:CP=DE
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O) Hai đường cao BD và CE cắt nhau tại H.Chứng minh rằng:
a.Tứ giác BEDC,AEHD là tứ giác nội tiếp;
b.DEC=DBC
c.Qua A vẽ tiếp tuyến xy của (O) chứng minh OA vuông góc với DE
Cho tam giác ABC nhọn nội tiếp đường tròn (O).
Các đường cao BD, CE của tam giác ABC cắt nhau tại H
và cắt đường tròn (O) lần lượt tại M và N. Chứng minh:
a. Các tứ giác ADHE, BEDC nội tiếp
b. DE/MN
c. OA.LDE
Cho tam giác ABC nhọn và có các đường cao BD, CE. Chứng minh:
a, Các điểm B, D, C, E cùng thuộc một đường tròn
b, BC > DE
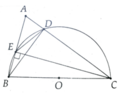
a, B,C,D,E cùng thuộc đường tròn đường kính BC
b, BC là đường kính, ED dây không qua tâm => ĐPCM
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao BD,CE cắt nhau tại H. DE cắt BC tại F. Gọi K là giao điểm của AF với (O),N là giao điểm của KH
a) Chứng minh tứ giá BEDC nội tiếp. Xác định tâm M của đường tròn ngoại tiếp tứ giác BEDC
b ) Chứng minh góc FKE góc FDA
c ) Chứng minh AN là đường kính của đường tròn tâm O từ đó suy ra FH vuông góc với AM
Đọc tiếp
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao BD,CE cắt nhau tại H. DE cắt BC tại F. Gọi K là giao điểm của AF với (O),N là giao điểm của KH
a) Chứng minh tứ giá BEDC nội tiếp. Xác định tâm M của đường tròn ngoại tiếp tứ giác BEDC
b ) Chứng minh góc FKE= góc FDA
c ) Chứng minh AN là đường kính của đường tròn tâm O từ đó suy ra FH vuông góc với AM
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O . Hai đường cao BD và CE của tam giác ABC cắt nhau tại H, đường thẳng BD cắt đường tròn (O) tại điểm thứ hai P , đường thẳng CE cắt đường tròn (O) tại điểm thứ hai Q. Chứng minh rằng:
1) BEDC là tứ giác nội tiếp,
b) HQ.HC = HP.HB
3) DE // PQ
giúp mình giải toán với ạ
CHO TAM GIÁC ABC NHỌN ( AB < AC ) HAI ĐƯỜNG CAO BD VÀ CE CẮT NHAU TẠI H. I LÀ TRUNG ĐIỂM BC. ĐƯỜNG TRÒN ĐI QUA B,E,I VÀ ĐƯỜNG TRÒN ĐI QUA C , D ,I CẮT NHAU TẠI K ( K KHÁC I )
a) cmr : BEDC , BHKC là các tứ giác nội tiếp
b) cmr : HK vuông góc với AI
c) DE cắt BC tại M . chứng minh M , H , K thẳng hàng
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R). Vẽ 2 đường cao BD và CE của tam giác ABC cắt nhau tại H, DE cắt (O) lần lượt tại P và Q (P thuộc cung nhỏ AB). 1/Chứng tỏ BEDC nội tiếp, xác đinh tâm của nó. 2/Chứng tỏ BH.DH=HE.HC. 3/Chứng tỏ tam giác APQ cân tại A và AP2=AE.AB. 4/Gọi S1 là diện tích tam giác APQ, S2 là diện tích tam giác ABC. Giả sử S1/S2=PQ/2BC. Tính BC theo R''.
Cho tam giác ABC nhọn nội tiếp đường tròn, đường cao BD,CE. CMR đường thẳng qua A vuông góc với DE đi qua 1 điểm cố định

