cho AB // CD, góc ABE 20 , góc AEC 60 .Tinh ECD A B 20 o 60 o C D E
Đọc tiếp
cho AB // CD, góc ABE =20 , góc AEC =60 .Tinh ECD
LL
Những câu hỏi liên quan
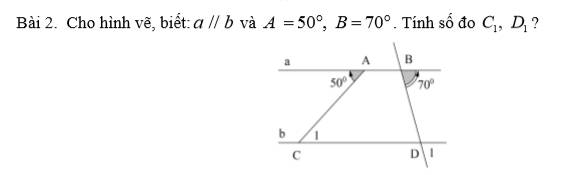
Tính số đo góc ECD biết AB song song với CD và góc BAE=40o; góc AEC=60o
Qua điểm E vẽ đường thẳng x song song với AB và CD
Ta có: góc BAE = AEx = 40o (so le trong)
Mặt khác: AEx + xEC = AEC
=> xEC = AEC - AEx = 60o - 40o = 20o
=> ECD = xEC = 20o (so le trong)
Vậy ECD = 20o
Đúng 0
Bình luận (0)
cho tam giác ABC = 600, AB = 6cm. Trên cạnh AB lấy điểm D (D khác A,B) sao cho AD = 2cm
a, Tính độ dài đoạn thẳng BD
b. Tính số đo của góc DCB biết góc ACD = 20o
c, Dựng tia Cx sao cho góc DCx = 90o. Tính góc ACx
đ, Trên cạnh AC lấy điểm E (E khác A,C). C/m 2 đoạn thẳng CD và BE cắt nhau
Tính số đo góc ECD, biết AB song song CD và góc BAE =40 độ,góc AEC=60 độ
giả sử AB cắt CE tại I. ta có góc EIB = góc EAI + góc AEI = 100 độ( góc ngoài tam giác AIE).
mà góc ECD = góc EIB ( hai góc đồng vị)
vậy góc ECD = 100 độ
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có góc B = 60o và AB = 5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC (E thuộc BC). Chứng minh:
a) Tam giác ABD = Tam giác EBD
b) Tam giác ABE là tam giác đều
c) Tam giác AEC cân
d) Tính độ dài cạnh AC
cho hình vễ bên,biết góc C= 60 độ gọc D =60 độ,c thuộc b tại B a)Chứng mình a//b b)Tính số đo góc D.1B tia phân giác của góc D.1B cắt CB tại E ,tính số đo góc của AEC c) Trên tia đối của tia EA lấy điểm K sao cho góc KBE = 20 độ,tính số đo góc AKB
cho hình vễ bên,biết góc C= 60 độ gọc D =60 độ,c thuộc b tại B a)Chứng mình a//b b)Tính số đo góc D.1B tia phân giác của góc D.1B cắt CB tại E ,tính số đo góc của AEC c) Trên tia đối của tia EA lấy điểm K sao cho góc KBE = 20 độ,tính số đo góc AKB
Giúp mk bài này với !!!
Tam giác ABC có góc B=60 độ, góc C=20 độ, BC =4. Gọi D là trung điểm của AC. Trên cạnh BC lấy điểm E sao cho CE=CD. Tính tổng diện tích các tam giác ECD và ABD.
Cho tứ giác ABCD biết AB= AD, góc B =90 độ, góc A = 60 độ, góc D= 135 độ. Cm: a) Tính góc và cm BD= BC. b) từ A kẻ AE vuông góc với CD tại E. Tính các góc của tam giác AEC
cho ΔABC vuông tại A, góc ABC=60\(^O\), tia p/ggóc ABC cắt AC tại D. Kể DEvuông góc BC (E ϵ BC). CM:
a, BE=BA
b, BD là trung trực của AE
c, AB<DC
a.Xét tam giác vuông ABD và tam giác vuông EBD, có:
AD: cạnh chung
góc ABD = góc EBD ( gt )
Vậy tam giác vuông ABD = tam giác vuông EBD(cạnh huyền.góc nhọn)
=> BE=BA ( 2 cạnh tương ứng )
b.=> AD = ED ( 2 cạnh tương ứng )
=> Tam giác DAE cân tại D
Mà góc BDA = góc BDE ( 2 góc tương ứng )
=> BD là trung trực của đoạn thẳng AE
Đúng 0
Bình luận (1)
cho ΔABC vuông tại A, góc ABC=60\(^o\), tia p/ggóc ABC cắt AC tại D. Kể DEvuông góc BC (E ϵ BC). CM:
a, BE=BA
b, BD là trung trực của AE
c, AB<DC
Hình vẽ
a) Do BD là tia phân giác của \(\widehat{BAC\left(gt\right)\Rightarrow}\) \(\widehat{ABD}=\widehat{DBC}hay\widehat{ABD}=\widehat{DBE}\)
Do \(DE\perp BC\left(gt\right)\Rightarrow\widehat{DEB}=\widehat{DEC}=90^o\)
Xét \(\Delta ABD\) và \(\Delta EDB\) có : \(\left\{{}\begin{matrix}\widehat{ABD}=\widehat{DBE}\left(cmt\right)\\BDchung\\\widehat{BAC}=\widehat{DEB}\left(=90^o\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABD=\Delta EDB\left(ch-gn\right)\)
\(\Rightarrow AB=BE\) ( 2 cạnh tương ứng )
Đúng 0
Bình luận (0)