Mún tìm GTNN của 1 đa thức đầu tiên phải biến đổi đa thức dưới dạng 1 hằng đẳng thức, VD:

Tìm GTNN A= x^2 + 4x - 1

=x^2 + 4x +4 -5

=(x +2)^2 -5 >= -5 Do (x + 2)^2 >= 0 với mọi x

Vậy GTNN của A = -5 <=> x + 2= 0

<=> x= -2

Đặt  \(A=x^2-3x\)

\(A=\left(x^2-3x+\frac{9}{4}\right)-\frac{9}{4}\)

\(A=\left(x-\frac{3}{2}\right)^2-\frac{9}{4}\)

Mà  \(\left(x-\frac{3}{2}\right)^2\ge0\forall x\)

\(\Rightarrow A\ge-\frac{9}{4}\)

Dấu "=" xảy ra khi :  \(x-\frac{3}{2}=0\Leftrightarrow x=\frac{3}{2}\)

Vậy  \(A_{Min}=-\frac{9}{4}\Leftrightarrow x=\frac{3}{2}\)

Đặt  \(B=-x^2-2x\)

\(-B=x^2+2x\)

\(-B=\left(x^2+2x+1\right)-1\)

\(-B=\left(x+1\right)^2-1\)

Mà  \(\left(x+1\right)^2\ge0\forall x\)

\(\Rightarrow-B\ge-1\Leftrightarrow B\le1\)

Dấu "=" xảy ra khi :  \(x+1=0\Leftrightarrow x=-1\)

Vậy  \(B_{Max}=1\Leftrightarrow x=-1\)

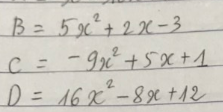
Lời giải:
$B=5x^2+2x-3=5(x^2+\frac{2}{5}x+\frac{1}{5^2})-\frac{16}{5}$

$=5(x+\frac{1}{5})^2-\frac{16}{5}$

$\geq 5.0-\frac{16}{5}=\frac{-16}{5}$
Vậy GTNN của $B$ là $\frac{-16}{5}$. Giá trị này đạt tại $x+\frac{1}{5}=0\Leftrightarrow x=-\frac{1}{5}$

---------------------------------

$C=-9x^2+5x+1=1-(9x^2-5x)$

$=\frac{61}{36}-[(3x)^2-2.3x.\frac{5}{6}+(\frac{5}{6})^2]$

$=\frac{61}{36}-(3x-\frac{5}{6})^2$

$\leq \frac{61}{36}$

Vậy gtln của $C$ là $\frac{61}{36}$. Giá trị này đạt tại $3x-\frac{5}{6}=0\Leftrightarrow x=\frac{5}{18}$

-----------------------

$D=16x^2-8x+12=(4x)^2-2.4x.1+1+11$

$=(4x-1)^2+11\geq 0+11=11$

Vậy gtnn của $D$ là $11$. Giá trị này đạt tại $4x-1=0\Leftrightarrow x=\frac{1}{4}$