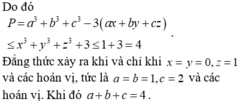điền chữ số a,b,c sao cho abc + bca đạt giá trị lớn nhất và a,b,c nhận các giá trị 1,2,3
H24
Những câu hỏi liên quan
điền chữ số a,b,c sao cho abc + bca đạt giá trị lớn nhất và a,b,c nhận các giá trị 1,2,3 ( ko nhất thiết phải tương ứng )
abc + bca = a . 100 + b . 10 + c + b . 100 + c . 10 + a = a . 101 + b . 110 + c . 11
Muốn abc + bca đạt giá trị lớn nhất thì b = 3 ( vì nhiều b nhất ) ; a = 2 và c = 1
Lúc này giá trị của abc + bca = 231 + 312 = 543
đ/s : ....
Đúng 0
Bình luận (0)
Ta có :n=abc+bca =101a+110b+11c
Để n lớn nhất ,ta chọn b=3,a=2,c=1
Ta được n=231+321=543
Đ/S:543
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
điền chữ số a,b,c sao cho abc + bca đạt giá trị lớn nhất và a,b,c nhận các giá trị 1, 2 ,3 < ko nhất thiết phải tương ứng>
Ta có \(n=\overline{abc}+\overline{bca}\)
\(=101a+101b+11c\)
Để n đạt giá trị lớn nhất thì ta chọn b = 3 , a =2 , c =1
ta được : n = 231 + 312 = 543
cho 2 dãy số tự nhiên 1,2,3,..,50
a, tìm 2 số thuoccj dãy trên sao cho ƯCLN của chúng đạt giá trị lớn nhất
b, tìm 2 số thuộc dãy trên sao cho BCNN cuả chúng đạt giá trị lớn nhất
a. Vậy hai số có UCLN đạt giá trị lớn nhất là 50 , 25
b. Vậy hai số có BCNN đạt giá trị lớn nhất là 50 , 49
Đúng 0
Bình luận (0)
thay các chữ bằng chữ số thích hợp sao cho \(\frac{abc}{a+b+c}\) nhận giá trị lớn nhất
8. Biết BCNN(a,b) = 385 và BCNN(a, c) = 84. Tìm a,b,c.
9. Cho dãy số tự nhiên 1; 2; 3;..; 100. Tìm hai số khác nhau thuộc dãy số trên, sao cho:
a) BCNN của chúng đạt giá trị lớn nhất
b) ƯCLN của chúng đạt giá trị lớn nhấ
Cho phân số 6n-4/2n+3
a, Tìm n để A nhận giá trị là số nguyên
B, Tìm n để A đạt giá trị lớn nhất và tính giá trị đó
Xem chi tiết
GTLN = 16
n = -2
nha bạn chúc bạn học tốt nha
gtln =16
n=-2
chúc bạn hok tốt
GTLN =16
n =-2
các bạn hộ mình nhé
mik cảm ơn
học tốt nhé
câu1:
a) Cho các số thực không âm a, b, c thỏa mãn a + b + c =1. Tìm giá trị lớn nhất và giá trị nhỏ
nhất của biểu thức:
P=\(\frac{ab+bc+ca-abc}{a+2b+c}\)
b) Cho các số thực a, b, c thỏa mãn \(^{a^2+b^2+c^2=1}\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P =ab +bc + ca .
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn . Khi biểu thức đạt giá trị lớn nhất thì giá trị của tổng a+b+c là A. 3 B.
3
.
2
1
3
3
C. 4 D. 6
Đọc tiếp
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn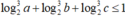 
. Khi biểu thức 
đạt giá trị lớn nhất thì giá trị của tổng a+b+c là
A. 3
B. 3 . 2 1 3 3
C. 4
D. 6
Cho phân số 6n-4/2n+3, n thuộc z
a, Tìm n để A nhận giá trị là số nguyên
b, Tìm n để A đạt giá trị lớn nhất và tính giá trị đó
Xem chi tiết
\(A=\frac{6n-4}{2n+3}=\frac{6n+9-13}{2n+3}=3-\frac{13}{2n+3}\)
a. Để A đạt giá trị nguyên thì \(\frac{13}{2n-3}\)đạt giá trị nguyên
=> 2n - 3\(\in\){ - 13 ; - 1 ; 1 ; 13 }
=> n\(\in\){ - 5 ; 1 ; 2 ; 8 }
b. thêm điều kiện n\(\in\)Z
Để A đạt GTLN thì \(\frac{13}{2n-3}\)đạt GTNN <=> 2n - 3 đạt GTLN ( không thể tìm được n )