Cho mệnh đề: "Với a = log2; b = log3. Ta viết được log26=\(\dfrac{\alpha a+b}{\beta a}\Rightarrow\alpha\beta=2\)"
Mệnh đề trên đúng hay sai? Giải thích.
NN
Những câu hỏi liên quan
Cho a, b, c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau: (I)
2
a
3
⇔
a
log
2
3
(II)
∀
x
∈
ℝ
0
,
log...
Đọc tiếp
Cho a, b, c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau:
(I) 2 a = 3 ⇔ a = log 2 3
(II) ∀ x ∈ ℝ \ 0 , log 3 x 2 = 2 log 3 x
(III) log a b . c = log a b . log a c
Trong ba mệnh đề (I), (II), (III), tổng số mệnh đề đúng là?
A. 3
B. 2
C. 1
D. 0
Đáp án C
Mệnh đề (I) đúng.
Mệnh đề (II) sai vì log3 x2 = 2log3 x > 0 khi x > 0 nên điều kiện ∀ x ∈ ℝ \ 0 chưa đủ.
Mệnh đề (III) sai vì loga (b.c) = loga b + loga c.
Số mệnh đề đúng là 1.
Đúng 0
Bình luận (0)
Xét các mệnh đề sau (1) log2(x - 1)2 + 2log2(x+1) 6 2log2(x-1) + 2log2(x+1) 6 (2) log2(x2+1)
≥
1 + log2|x|;
∀
x
∈
R
(3) xlny ylnx;
∀
x
y
2
(
4
)
log
2
2
2
x
-
4
log...
Đọc tiếp
Xét các mệnh đề sau
(1) log2(x - 1)2 + 2log2(x+1) = 6
<=> 2log2(x-1) + 2log2(x+1) = 6
(2) log2(x2+1) ≥ 1 + log2|x|; ∀ x ∈ R
(3) xlny = ylnx; ∀ x > y > 2
( 4 ) log 2 2 2 x - 4 log 2 x - 4 = 0 ⇔ log 2 2 x - 4 log 2 x - 3 = 0
Số mệnh đề đúng là
A. 0
B. 1
C. 2
D. 3
Đáp án C
Dựa vào giả thiết, ta thấy rằng:
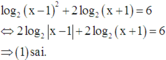
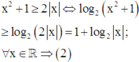
đúng.
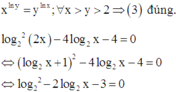
=> (4) sai. Vậy có 2 mệnh đề đúng.
Đúng 0
Bình luận (0)
Biết rằng phương trình
2
+
5
x
+
1
8
5
-
2
2
x
-
1
có nghiệm duy nhất dạng
log...
Đọc tiếp
Biết rằng phương trình 2 + 5 x + 1 = 8 5 - 2 2 x - 1 có nghiệm duy nhất dạng log 2 + 5 a , với a là số thực dương. Mệnh đề nào dưới đây là đúng?
A. 0 < a < 4/5
B. 5 < a < 9
C. 4/5 < a < 12/5
D. 3 < a < 7/2
Chọn C.
Ta có: ![]() nên phương trình
nên phương trình 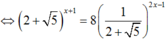
![]()
![]()
![]()
![]()
Do đó a = 2.
Đúng 0
Bình luận (0)
Cho mệnh đề “Nếu a và b là những số thực dương thì tích ab 0”. Mệnh đề tương đương với mệnh đề đã cho là: A. Điều kiện cần để tích ab 0 là a và b là những số thực dương. B. Điều kiện đủ để tích ab 0 là a và b là những số thực dương C. Điều kiện đủ để a và b là những số thực dương là tích ab 0 D. Cả B, C đều đúng
Đọc tiếp
Cho mệnh đề “Nếu a và b là những số thực dương thì tích ab > 0”. Mệnh đề tương đương với mệnh đề đã cho là:
A. Điều kiện cần để tích ab > 0 là a và b là những số thực dương.
B. Điều kiện đủ để tích ab > 0 là a và b là những số thực dương
C. Điều kiện đủ để a và b là những số thực dương là tích ab > 0
D. Cả B, C đều đúng
Đáp án: B
P: “a và b là những số thực dương”; Q: “tích ab > 0”.
Mệnh đề đã cho: P => Q. Nghĩa là, Điều kiện đủ để có Q là P hay Điều kiện cần để có P là Q. Do đó B đúng
Đúng 0
Bình luận (0)
Cho n là số tự nhiên. Xét các mệnh đề:
P: “n là một số tự nhiên chia hết cho 16”.
Q: “n là một số tự nhiên chia hết cho 8”.
a) Với n = 32, phát biểu mệnh đề P ⇒ Q và xét tính đúng sai của mệnh đề đó.
b) Với n = 40, phát biểu mệnh đề đảo của mệnh đề P ⇒ Q và xét tính đúng sai của mệnh đề đó.
a) Với n = 32, ta có các mệnh đề P, Q khi đó là:
P: “Số tự nhiên 32 chia hết cho 16”;
Q: “Số tự nhiên 32 chia hết cho 8”;
Mệnh đề P ⇒ Q: “Nếu số tự nhiên 32 chia hết cho 16 thì số tự nhiên 32 chia hết cho 8”.
Đây là mệnh đề đúng vì 32 chia hết cho 16 và 8.
b) Với n = 40, ta có các mệnh đề P, Q khi đó là:
P: “Số tự nhiên 40 chia hết cho 16”;
Q: “Số tự nhiên 40 chia hết cho 8”;
Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P: “Nếu số tự nhiên 40 chia hết cho 8 thì số tự nhiên 40 chia hết cho 16”.
Mệnh đề đảo này là mệnh đề sai. Vì 40 chia hết cho 8 nhưng 40 không chia hết cho 16.
Đúng 0
Bình luận (0)
Cho hai số thực a và b sao cho với
a
-
5
a
-
4
và
log
b
3
4
log
b
4
5
. Trong các mệnh đề sau mệnh đề nào là đúng? A. a 1; b 1 B. a 1; 0 b 1 C. 0 a 1; b...
Đọc tiếp
Cho hai số thực a và b sao cho với a - 5 > a - 4 và log b 3 4 < log b 4 5 . Trong các mệnh đề sau mệnh đề nào là đúng?
A. a > 1; b > 1
B. a > 1; 0 < b < 1
C. 0 < a < 1; b > 1
D. 0 < a < 1; 0 < b < 1
Ta có - 5 < - 4 a - 5 > a - 4 ⇒ 0 < a < 1
và
3 4 < 4 5 log b 3 4 < log b 4 5 ⇒ b > 1
Vậy 0 < a < 1; b > 1
Đáp án C
Đúng 0
Bình luận (0)
Trong 4 mệnh đề sau có 2 mệnh đề đúng và 2 mệnh đế sai, mệnh đề 1 A chia hết cho 6, mệnh đề 2 A chia hết cho 23, mệnh đề 3 A+7 là số chính phương, mệnh đề 4 A-10 là số chính phương. Tìm A
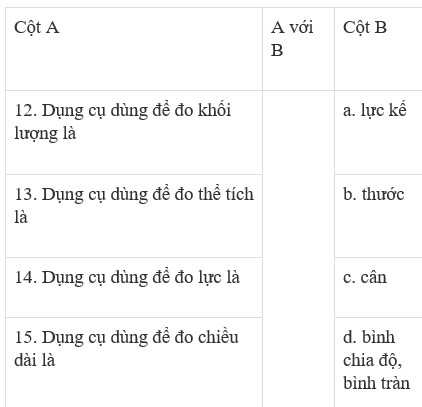
Nối mỗi mệnh đề ở cột A với mỗi mệnh đề ở cột B sao cho thành một câu đúng
Cho mệnh đề: Với mọi số nguyên n không chia hết cho 3,
n
2
−
1
chia hết cho 3. Mệnh đề phủ định của mệnh đề trên là mệnh đề nào dưới đây? A. Tồn tại số nguyên n không chia hết cho 3,
n
2
−
1
không chia hết cho 3; B. Tồn tại số nguyên n không chia hết cho 3,
n
2
−
1
chia hết cho 3; C. Tồn tại số nguyên n chia hết c...
Đọc tiếp
Cho mệnh đề: "Với mọi số nguyên n không chia hết cho 3, n 2 − 1 chia hết cho 3". Mệnh đề phủ định của mệnh đề trên là mệnh đề nào dưới đây?
A. "Tồn tại số nguyên n không chia hết cho 3, n 2 − 1 không chia hết cho 3";
B. "Tồn tại số nguyên n không chia hết cho 3, n 2 − 1 chia hết cho 3";
C. "Tồn tại số nguyên n chia hết cho 3, n 2 − 1 chia hết cho 3";
D. "Tồn tại số nguyên n chia hết cho 3, n 2 − 1 không chia hết cho 3";
Mệnh đề: "Với mọi số nguyên n không chia hết cho 3, n 2 − 1 chia hết cho 3".
Mệnh đề phủ định của mệnh đề trên là "Tồn tại số nguyên n không chia hết cho 3, n 2 − 1 không chia hết cho 3".
Mệnh đề phủ định của mệnh đề " ∀ x ∈ X ; P ( x ) " là " ∃ x ∈ X ; P ( x ) ¯ "
Đáp án A
Đúng 0
Bình luận (0)
Xét hai mệnh đề dạng \(P \Rightarrow Q\) sau:
“Nếu ABC là tam giác đều thì nó có hai góc bằng \({60^o}\)”;
“Nếu \(a = 2\) thì \({a^2} - 4 = 0\)”.
a) Chỉ ra P, Q và xét tính đúng sai của mỗi mệnh đề trên.
b) Với mỗi mệnh đề đã cho, phát biểu mệnh đề \(Q \Rightarrow P\) và xét tính đúng sai của nó.
a)
+) Mệnh đề R: “Nếu ABC là tam giác đều thì nó có hai góc bằng \({60^o}\)” có dạng \(P \Rightarrow Q\), với
P: “ABC là tam giác đều” và Q: “Tam giác ABC có hai góc bằng \({60^o}\)”
Ta thấy khi P đúng thì Q cũng đúng. Do đó \(P \Rightarrow Q\) đúng hay R đúng.
+) Mệnh đề T: “Nếu \(a = 2\) thì \({a^2} - 4 = 0\)” có dạng \(P \Rightarrow Q\), với:
P: “\(a = 2\)” và Q: “\({a^2} - 4 = 0\)”.
Ta thấy khi P đúng thì Q cũng đúng. Do đó \(P \Rightarrow Q\) đúng hay T đúng.
b) Mệnh đề \(Q \Rightarrow P\) của hai mệnh đề trên là:
“Nếu ABC có hai góc bằng \({60^o}\) thì nó là tam giác đều”, đúng.
“Nếu \({a^2} - 4 = 0\) thì \(a = 2\)” sai (vì thiếu nghiệm \(a = - 2\)).
Đúng 0
Bình luận (0)

