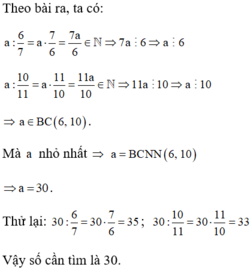Tìm số tự nhiên nhỏ nhất sao cho
là các số nguyên tố. Kết quả là
PH
Những câu hỏi liên quan
Tìm số tự nhiên n nhỏ nhất sao cho : n; ; n + 2 ; n + 6 là các số nguyên tố . Kết quả n =
Điền kết quả thích hợp vào chỗ (...):Câu 1:Số các ước tự nhiên có hai chữ số của 45 là Câu 2:Tập hợp các số có hai chữ số là bội của 41 là {} (Nhập các phần tử theo giá trị tăng dần, ngăn cách bởi dấu ;).Câu 3:Tập hợp các số tự nhiên sao cho là {} (Nhập các phần tử theo giá trị tăng dần, ngăn cách bởi dấu ;).Câu 4:Viết số 43 dưới dạng tổng của hai số nguyên tố với . Khi đó Câu 5:Tìm số nguyên tố sao cho và cũng là số nguyên tố.Kết quả là Câu 6:Tìm số nguyên tố sao cho và cũng là số ng...
Đọc tiếp
Điền kết quả thích hợp vào chỗ (...):
Câu 1:
Số các ước tự nhiên có hai chữ số của 45 là
Câu 2:
Tập hợp các số có hai chữ số là bội của 41 là {} (Nhập các phần tử theo giá trị tăng dần, ngăn cách bởi dấu ";").
Câu 3:
Tập hợp các số tự nhiên sao cho là {} (Nhập các phần tử theo giá trị tăng dần, ngăn cách bởi dấu ";").
Câu 4:
Viết số 43 dưới dạng tổng của hai số nguyên tố với . Khi đó
Câu 5:
Tìm số nguyên tố sao cho và cũng là số nguyên tố.
Kết quả là
Câu 6:
Tìm số nguyên tố sao cho và cũng là số nguyên tố.
Kết quả là
Câu 7:
Cho là chữ số khác 0. Khi đó
Câu 8:
Số số nguyên tố có dạng là
Câu 9:
Có bao nhiêu số nguyên tố có dạng ?
Trả lời: số.
Câu 10:
Tìm số tự nhiên a nhỏ nhất khác 5 biết khi chia a cho 12; cho 15 và cho 18 đều dư 5. Vậy a = .
Tìm số tự nhiên n nhỏ nhất sao cho n, n +2, n+ 6 là các số nguyên tố.
Các số nguyên tố là các số tự nhiên lớn hơn 1 chỉ có 2 ước là 1 và chinh nó
=> n không bằng 1
Đúng 0
Bình luận (0)
Tìm số tự nhiên nhỏ nhất a khác 0 sao cho khi chia a cho các phân số 11/18 và 25/6 ta đều được kết quả là các số tự nhiên
Theo đề bài ta có : a/(11/18) = a*(18/11) thuộc N suy ra 18*a chia hết cho 11.
Lại có : a/(25/6) = a*(6/25) thuộc N suy ra 6*a chia hết cho 25.
Như vậy, a là bội chung của 11 và 25 nhưng để a nhỏ nhất thì a = BCNN (11, 25) = 275.
Vậy số cần tìm là 275 bạn nhé!
Chúc bạn học tốt!
Tìm số tự nhiên n sao cho (n - 2)(n^2 + n - 1) là số nguyên tố. Kết quả n =......
do biểu thức trên là số nguyên tố nên chỉ có hai ước là 1 và chính nó
nhận thấy n-2 < n2+n-1
=> n-2=1
n=3
thay vào ta được số nguyên tố là 11
Đúng 0
Bình luận (0)
1.Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho 7,cho 13,cho 17có số dư lần lượt là 3,11,14.2.Tìm 2 số tự nhiên a và b (ab) biết BCNN (a,b) + ƯCLN (a,b) 193.Tìm tất cả những cặp số tự nhiên (x;y) sao cho 6x +9920y4.Tổng của 38 số tự nhiên lẻ liên tiếp bằng 2052.Tìm số nhỏ nhất.5.Cho A4 + 42 + ................489Tìm số dư khi chia A cho 856.1xy là bội của 9 và là số nguyên tố nhỏ nhất .Tìm x,y7.Tìm số nguyên tố P sao cho các số sau cũng là số nguyên tố : P+2 và P+10GIÚP MÌNH VỚI , BIẾT LÀM...
Đọc tiếp
1.Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho 7,cho 13,cho 17có số dư lần lượt là 3,11,14.
2.Tìm 2 số tự nhiên a và b (a<b) biết BCNN (a,b) + ƯCLN (a,b) = 19
3.Tìm tất cả những cặp số tự nhiên (x;y) sao cho 6x +99=20y
4.Tổng của 38 số tự nhiên lẻ liên tiếp bằng 2052.Tìm số nhỏ nhất.
5.Cho A=4 + 42 + ................489
Tìm số dư khi chia A cho 85
6.1xy là bội của 9 và là số nguyên tố nhỏ nhất .Tìm x,y
7.Tìm số nguyên tố P sao cho các số sau cũng là số nguyên tố : P+2 và P+10
GIÚP MÌNH VỚI , BIẾT LÀM BÀI NÀO THÌ CỨ LÀM ,KHÔNG BIẾT THÌ KHÔNG SAO
AI NHANH NHẤT VÀ ĐÚNG NHẤT MÌNH TICK CHO 2 TICK ! ! ! ! !
1. Ta có: a chia có 7 dư 3 => a - 3 chia hết cho 7
=> 4 (a - 3) chia hết cho 7 => 4a - 12 chia hết cho 7
=> 4a - 12 + 7 chia hết cho 7 => 4a - 5 chia hết cho 7 (1)
a chia cho 13 dư 11 => a - 11 chia hết cho 13
=> 4 (a - 11) chia hết cho 13 => 4a - 44 chia hết cho 13
=> 4a - 44 + 39 chia hết cho 13 => 4a - 5 chia hết cho 13 (2)
a chia cho 17 dư 14 => a - 14 chia hết cho 17
=> 4 ( a - 14) chia hết cho 17 => 4a - 56 chia hết cho 17
=> 4a - 56 + 51 chia hết cho 17 => 4a - 5 chia hết cho 17 (3)
Từ (1), (2) và (3) => 4a - 5 thuộc BC(7;13;17)
Mà a nhỏ nhất => 4a - 5 nhỏ nhất
=> 4a - 5 = BCNN(7;13;17) = 7 . 13 . 17 = 1547
=> 4a = 1552 => a= 388
2. Gọi ƯCLN(a,b) = d
=> a = d . m (ƯCLN(m,n) = 1)
b = d . n
Do a < b => m<n
Vì BCNN(a,b) . ƯCLN(a,b) = a . b
\(\Rightarrow BCNN\left(a,b\right)=\frac{a\cdot b}{ƯCLN\left(a,b\right)}=\frac{d\cdot m\cdot d\cdot n}{d}=m\cdot n\cdot d\)
Vì BCNN(a,b) + ƯCLN(a,b) = 19
=> m . n . d + d = 19
=> d . (m . n + 1) = 19
=> m . n + 1 thuộc Ư(19); \(m\cdot n+1\ge2\)
Ta có bảng sau:
Vậy (a,b) = (2;9) ; (1 ; 18)
3.
1) Tìm số tự nhiên nhỏ nhất chia cho 5 dư 1, chia cho 7 dư 3.
2) Tìm số nguyên tố p sao cho p2 +4 và p2– 4 đều là số nguyên tố.
Gọi số cần tìm là a ( a ∈ N)
Ta có:
a chia 5 dư 1
⇒ a+4 chia hết cho 5
a chia 7 dư 3
⇒ a+4 chia hết cho 7
Mà (5,7) = 1
⇒ a+4 chia hết cho 35
Vì a là số tự nhiên nhỏ nhất
⇒a+4 = 35
⇒a=35-4
⇒a=31
Vậy số tự nhiên cần tìm là 31
Đúng 0
Bình luận (0)
1)Gọi số x là số tự nhiên nhỏ nhất cần tìm, theo đề bài ta có :
x=5a+1 ; x=7b+3
Nên 5a+1=7b+3
5a-7b=2
Ta thấy 5.6-7.4=2
Nên a=6; b=4
Vậy x=31
2) Theo đề bài : p2 + 4 và p2 - 4 đều là số nguyên tố
⇒ (p2 + 4) và (p2 - 4) ⋮ 1 và chính nó
⇒ (p2 + 4) và (p2 - 4) ϵ {1;2;3;5;7;11;13...}
Ta thấy khi (p2 + 4) = 13 và (p2 - 4) = 5 thì p=3
Vậy p=3
Đúng 0
Bình luận (0)
Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho 6 7 và chia a cho 10 11 ta đều được kết quả là số tự nhiên.
Bài 1: Tim so nguyên tố P để có:
a) P+10 và P+14 là số nguyên tố
b) P+2; P+6 và P+8 là số nguyên tố
c) P+6; P+12; P+24 và P+38 là số nguyên tố
d) P+2; P+4 là số nguyên tố
Bài 2: Tìm số tự nhiên nhỏ nhất chia cho 5, cho 7, cho 9 dư là 3; 4; 5
Bài 3: Tìm số tự nhiên nhỏ hơn 500 sao cho chia nó cho 15, cho 35 được các só dư là 8 và 13
Thanks